题目内容
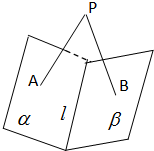如图，p是二面角α-l-β内的一点（p∉α，p∉β），PA⊥α于点A，PB⊥β于点B，∠APB=35°，则二面角α-l-β的大小是考点：二面角的平面角及求法
专题：空间角
分析：如图所示，平面PAB与l相交于点O，连接OA，OB．由于PA⊥α于点A，可得PA⊥l．同理可得PB⊥l．可得l⊥平面PAOB．可得∠AOB是二面角α-l-β的平面角．即可得出．
解答：
解：如图所示，平面PAB与l相交于点O，连接OA，OB．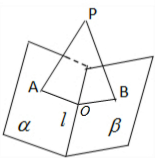
∵PA⊥α于点A，
∴PA⊥l．
同理可得PB⊥l．
又PA∩PB=P．
∴l⊥平面PAOB．
∴l⊥OA，l⊥OB．
∴∠AOB是二面角α-l-β的平面角．
∵∠APB=35°，
∴∠AOB=145°．
故答案为：145°．
∵PA⊥α于点A，
∴PA⊥l．
同理可得PB⊥l．
又PA∩PB=P．
∴l⊥平面PAOB．
∴l⊥OA，l⊥OB．
∴∠AOB是二面角α-l-β的平面角．
∵∠APB=35°，
∴∠AOB=145°．
故答案为：145°．
点评：本题考查了线面垂直的判定与性质定理、二面角的平面角、四边形的内角和定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
步步高达标卷系列答案
相关题目
已知等差数列{an}的前n项和为Sn，a5=5，S5=15，则数列{
}的前200项和为（ ）
| 1 |
| anan-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在单位圆中，用三角形的重心公式