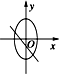题目内容
已知函数f(x)=lg(
+a),其中a为常数,且a≥-2.
(1)求函数f(x)的定义域;
(2)若函数f(x)为奇函数,①求a的值;②求函数g(x)=f(x)-lg(m-x)的零点个数.
| 2x |
| 2+x |
(1)求函数f(x)的定义域;
(2)若函数f(x)为奇函数,①求a的值;②求函数g(x)=f(x)-lg(m-x)的零点个数.
考点:根的存在性及根的个数判断,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)由
+a>0,可得
>0,分类讨论求得此不等式的解集,可得函数的定义域.
(2)①由于函数f(x)为奇函数,可得f(x)+f(-x)=0,化简可得 (2+a2)x2-4a2=x2-4,可得
,由此求得a的值.
②由以上可得,f(x)=lg
,令g(x)=0,可得m=x+
,令t=x+2 (t>4,或 t<0),可得m+1=t-
.画出函数y=m+1,和 y=t-
的图象,数形结合求得这两个函数的图象的交点个数,可得g(x)的零点个数.
| 2x |
| 2+x |
| (a+2)x+2a |
| x+2 |
(2)①由于函数f(x)为奇函数,可得f(x)+f(-x)=0,化简可得 (2+a2)x2-4a2=x2-4,可得
|
②由以上可得,f(x)=lg
| x-2 |
| x+2 |
| x-2 |
| x+2 |
| 4 |
| t |
| 4 |
| t |
解答:
 解:(1)由
解:(1)由
+a>0,
可得
>0,
当a=-2时,不等式即
>0,
求得x<-2,
故函数的定义域为(-∞,-2).
当a>-2时,由于-2-(-
)=
<0,∴-2<-
,
故不等式的解集为
{x|x<-2,或 x>-
},
故函数的定义域为{x|x<-2,或 x>-
}.
综上所述,当a=-2时,函数f(x)定义域为{x|x<-2};
当a>-2时,函数f(x)定义域为{x|x<-2,或 x>-
}.
(2)①由于函数f(x)为奇函数,可得f(x)+f(-x)=0,
即lg(
+a)+lg(
+a)=lg[(
+a)(
+a)=0,
∴(
+a)(
+a)=1,化简可得 (2+a2)x2-4a2=x2-4,∴
,求得a=-1.
②由以上可得,f(x)=lg(
+a)=lg
,
∴函数g(x)=f(x)-lg(m-x)=lg
-lg(m-x).
令g(x)=0,可得 lg
=lg(m-x),即
=m-x,即m=x+
(x<-2,或 x>2).
令t=x+2 (t>4,或 t<0),则m=(t-2)+
=t-
-1,即m+1=t-
.
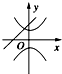
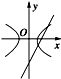
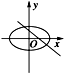
画出函数y=m+1,和 y=t-
的图象,如图所示:
当m+1≤3时,函数y=m+1,和 y=t-
的图象只有一个交点,函数g(x)仅有一个零点;
当m+1>3时,函数y=m+1,和 y=t-
的图象有两个交点,函数g(x)有两个零点.
 解:(1)由
解:(1)由| 2x |
| 2+x |
可得
| (a+2)x+2a |
| x+2 |
当a=-2时,不等式即
| -4 |
| x+2 |
求得x<-2,
故函数的定义域为(-∞,-2).
当a>-2时,由于-2-(-
| 2a |
| a+2 |
| -4 |
| a+2 |
| 2a |
| a+2 |
故不等式的解集为
{x|x<-2,或 x>-
| 2a |
| a+2 |
故函数的定义域为{x|x<-2,或 x>-
| 2a |
| a+2 |
综上所述,当a=-2时,函数f(x)定义域为{x|x<-2};
当a>-2时,函数f(x)定义域为{x|x<-2,或 x>-
| 2a |
| a+2 |
(2)①由于函数f(x)为奇函数,可得f(x)+f(-x)=0,
即lg(
| 2x |
| 2+x |
| -2x |
| 2-x |
| 2x |
| 2+x |
| -2x |
| 2-x |
∴(
| 2x |
| 2+x |
| -2x |
| 2-x |
|
②由以上可得,f(x)=lg(
| 2x |
| 2+x |
| x-2 |
| x+2 |
∴函数g(x)=f(x)-lg(m-x)=lg
| x-2 |
| x+2 |
令g(x)=0,可得 lg
| x-2 |
| x+2 |
| x-2 |
| x+2 |
| x-2 |
| x+2 |
令t=x+2 (t>4,或 t<0),则m=(t-2)+
| t-4 |
| t |
| 4 |
| t |
| 4 |
| t |
画出函数y=m+1,和 y=t-
| 4 |
| t |
当m+1≤3时,函数y=m+1,和 y=t-
| 4 |
| t |
当m+1>3时,函数y=m+1,和 y=t-
| 4 |
| t |
点评:本题主要考查函数的定义域和奇偶性,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列{
}的前200项和为( )
| 1 |
| anan-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|