题目内容
4.将全体正奇数排成一个三角形数阵:$\begin{array}{l}1&{\;}&{\;}&{\;}&{\;}&{\;}\\ 3&5&{\;}&{\;}&{\;}&{\;}\\ 7&9&{11}&{\;}&{\;}&{\;}\\{13}&{15}&{17}&{19}&{\;}&{\;}\\{…}&{\;}&{\;}&{\;}&{\;}&{\;}\end{array}$
按照以上规律的排列,求第n(n≥3)行从右到左的第三个数为n2+n-5.
分析 由三角形数阵,知第n+1行(n≥3)前共有1+2+3+…+n=$\frac{n(n+1)}{2}$个连续奇数,求出最后一个数字,即可得到结论
解答 解:观察三角形数阵,知第n+1行(n≥3)前共有1+2+3+…+n=$\frac{n(n+1)}{2}$个连续奇数,第n+1行(n≥3)最后的一个数字为n(n+1)+1=n2+n+1
故第n(n≥3)行从右到左的第三个数为n2+n+1-2×3=n2-n+5
故答案为:n2+n-5.
点评 本题从观察数阵的排列规律,考查了数列的求和应用问题;解题时,关键是发现规律并应用所学知识,来解答问题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
15.如图是2017年第一季度五省GDP情况图,则下列陈述正确的是( )
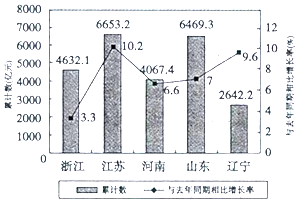
①2017年第一季度GDP总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长;
③去年同期的GDP总量前三位是江苏、山东、浙江;
④2016年同期浙江的GDP总量也是第三位.

①2017年第一季度GDP总量和增速均居同一位的省只有1个;
②与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长;
③去年同期的GDP总量前三位是江苏、山东、浙江;
④2016年同期浙江的GDP总量也是第三位.
| A. | ①② | B. | ②③④ | C. | ②④ | D. | ①③④ |
19. 在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则$\frac{1}{{h}_{1}^{2}}$=$\frac{1}{C{A}^{2}}$+$\frac{1}{C{B}^{2}}$;类比此性质,如图,在四面体P-ABC中,若PA,PB,PC两两相垂直,底面ABC上的高为h,则得到的正确结论为( )
在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则$\frac{1}{{h}_{1}^{2}}$=$\frac{1}{C{A}^{2}}$+$\frac{1}{C{B}^{2}}$;类比此性质,如图,在四面体P-ABC中,若PA,PB,PC两两相垂直,底面ABC上的高为h,则得到的正确结论为( )
 在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则$\frac{1}{{h}_{1}^{2}}$=$\frac{1}{C{A}^{2}}$+$\frac{1}{C{B}^{2}}$;类比此性质,如图,在四面体P-ABC中,若PA,PB,PC两两相垂直,底面ABC上的高为h,则得到的正确结论为( )
在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则$\frac{1}{{h}_{1}^{2}}$=$\frac{1}{C{A}^{2}}$+$\frac{1}{C{B}^{2}}$;类比此性质,如图,在四面体P-ABC中,若PA,PB,PC两两相垂直,底面ABC上的高为h,则得到的正确结论为( )| A. | $\frac{1}{h}$=$\frac{1}{PA}$+$\frac{1}{PB}$+$\frac{1}{PC}$ | B. | $\frac{1}{{h}^{2}}$=$\frac{1}{P{A}^{2}}$+$\frac{1}{P{B}^{2}}$+$\frac{1}{P{C}^{2}}$ | ||
| C. | $\frac{1}{{h}^{3}}$=$\frac{1}{P{A}^{3}}$+$\frac{1}{P{B}^{3}}$+$\frac{1}{P{C}^{3}}$ | D. | $\frac{1}{{h}^{4}}$=$\frac{1}{P{A}^{4}}$+$\frac{1}{P{B}^{4}}$+$\frac{1}{P{C}^{4}}$ |
9.某公司出售某种商品,统计了这种商品的销售价x(万元/吨)与月销售量y(吨)的关系 如表:
$\left\{\begin{array}{l}b=\frac{{\sum_{i=1}^n{(x_i-\overline x)(y_i-\overline y)}}}{{\sum_{i=1}^n{{{(x}_i-\overline x)}^2}}}\\ a=\overline y-b\overline x\end{array}\right.$
(1)已知y与x有关相关关系,并且可以用y=bx2+a来拟合,根据表中数据,建立y关于x 的回归方程;(b,a的结果保留整数位)
(2)已知这种商品的进价为2万元/吨,月利润为z万元,问销售价x(单位:万元/吨)为多少时,利润z最大?(精确到0.01,$\sqrt{3.04}=1.744$)
| X(万元) | 3 | 4 | 5 | 6 | 7 |
| Y(吨) | 90 | 83 | 75 | 65 | 52 |
(1)已知y与x有关相关关系,并且可以用y=bx2+a来拟合,根据表中数据,建立y关于x 的回归方程;(b,a的结果保留整数位)
(2)已知这种商品的进价为2万元/吨,月利润为z万元,问销售价x(单位:万元/吨)为多少时,利润z最大?(精确到0.01,$\sqrt{3.04}=1.744$)
13.某学校为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩(折算成了百分制),规定成绩在85分以上(含85分)为优秀.列联表如下:
(1)将列联表补充完整;
(2)若在这20名学生中任意选择一人参加比赛,求其物理和数学成绩都优秀的概率;
(3)能否在犯错误的概率不超过0.01的前提下认为物理成绩与数学成绩有关系?(参考公式及参考数据见卷首)
| 数学成绩优秀(人) | 数学成绩不优秀(人) | 合计 | |
| 物理成绩优秀(人) | a=5 | b=2 | a+b=7 |
| 物理成绩不优秀(人) | c=1 | d=12 | c+d=13 |
| 合计 | a+c=6 | b+d=14 | n=a+b+c+d=20 |
(2)若在这20名学生中任意选择一人参加比赛,求其物理和数学成绩都优秀的概率;
(3)能否在犯错误的概率不超过0.01的前提下认为物理成绩与数学成绩有关系?(参考公式及参考数据见卷首)