题目内容
18. 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.(Ⅰ)证明:A1C∥平面BC1D;
(Ⅱ)若A1A=A1C,点A1在平面ABC的射影在AC上,且侧面A1ABB1的面积为$2\sqrt{3}$,求三棱锥A1-BC1D的体积.
分析 (I)连接B1C交BC1于点E,连接DE.利用中位线定理可得DE∥A1C,故而A1C∥平面BC1D;
(II)过点A1作A1O⊥平面ABC,垂足为O,则O为AC中点,利用勾股定理计算A1O,代入体积公式V${\;}_{{A}_{1}-B{C}_{1}D}$=V${\;}_{B-{A}_{1}{C}_{1}D}$=$\frac{1}{3}{S}_{△{A}_{1}{C}_{1}D}•h$计算.
解答 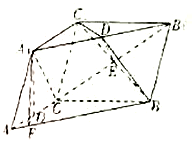 (Ⅰ)证明:连接B1C交BC1于点E,连接DE.
(Ⅰ)证明:连接B1C交BC1于点E,连接DE.
则E为B1C的中点,又D为A1B1的中点,
∴DE∥A1C,又DE?平面BC1D,A1C?平面BC1D,
∴A1C∥平面BC1D.
(Ⅱ)解:过点A1作A1O⊥平面ABC,垂足为O,则O在AC上,
∵A1A=A1C,∴O为AC的中点.
过点O作OF⊥AB于点F,连接A1F.
∵A1O⊥平面ABC,∴A1O⊥AB,
又A1O∩OF=O,A1D?平面A1OF,OF?平面A1OF,
∴AB⊥平面A1OF,∴A1F⊥AB.
∴侧面A1ABB1的面积为AB•A1F=2$\sqrt{3}$,
在△ABC中,AC=BC=2,∠ACB=120°,∴AB=2$\sqrt{3}$,
∴A1F=1,又AO=$\frac{1}{2}$AC=1,∠BAC=30°,
∴OF=$\frac{1}{2}$,AF=$\frac{\sqrt{3}}{2}$,
设A1O=h,则AA1=$\sqrt{{h}^{2}+1}$,
由AA12=AF2+A1F2可得h2+1=$\frac{3}{4}+1$,解得h=$\frac{\sqrt{3}}{2}$.
∴V${\;}_{{A}_{1}-B{C}_{1}D}$=V${\;}_{B-{A}_{1}{C}_{1}D}$=$\frac{1}{3}{S}_{△{A}_{1}{C}_{1}D}•h$=$\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}$=$\frac{1}{4}$.
点评 本题考查了线面平行的判定,线面垂直的判定,棱锥的体积计算,属于中档题.

| A. | (-∞,-1) | B. | (1,2) | C. | {2,5} | D. | {x|x2≤1} |
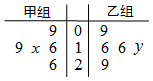 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )| A. | 7、8 | B. | 5、7 | C. | 8、5 | D. | 7、7 |
| A. | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ |