题目内容
8.设a≥b>0,分别用综合法和分析法证明:3a3+2b3≥3a2b+2ab2.分析 综合法:利用作差法分析符号,推出结果即可.
分析法:利用分析法的证明步骤,找出不等式成立的充要条件即可.
解答 证明:综合法:3a3+2b3-(3a2b+2ab2)=3a2(a-b)+2b2(b-a)=(3a2-2b2)(a-b).
因为a≥b>0,所以a-b≥0,3a2-2b2>0,从而(3a2-2b2)(a-b)≥0,
所以3a3+2b3≥3a2b+2ab2.…(6分)
分析法:要证3a3+2b3≥3a2b+2ab2,只需证3a2(a-b)-2b2(a-b)≥0,
只需证(3a2-2b2)(a-b)≥0,∵a≥b>0.∴a-b≥0,
3a2-2b2>2a2-2b2≥0,
即:3a3+2b3≥3a2b+2ab2…(6分)
点评 本题考查不等式的证明,分析法以及综合法的应用,考查逻辑推理能力.

练习册系列答案
相关题目
19.在等差数列{an}中,已知a2+a5=4,an=33,a1=$\frac{1}{3}$,则n是( )
| A. | 48 | B. | 49 | C. | 50 | D. | 51 |
16.某几何体的三视图如图所示,则该几何体的体积为( )
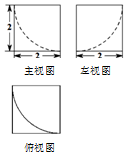

| A. | $8-\frac{4}{3}π$ | B. | $8-\frac{8}{3}π$ | C. | 24-π | D. | 24+π |
20.在等差数列{an}中,若a1,a3,a4成等比数列,则该等比数列的公比为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 1或$\frac{1}{2}$ | D. | 无法确定 |
 在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.
在三棱柱ABC-A1B1C1中,AC=BC=2,∠ACB=120°,D为A1B1的中点.