题目内容
9.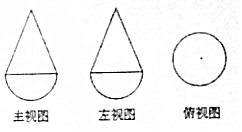 已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | $\frac{10π}{3}$ |
分析 由三视图知,此组合体上部是一个圆锥,下部是一个半球,半球体积易求,欲求圆锥体积需先求圆锥的高,再由公式求体积,最后再想加求出组合体的体积.
解答 解:这个几何体上部为一圆锥,下部是一个半球,
由于半球的半径为1,故其体积为$\frac{1}{2}×\frac{4}{3}$π×13=$\frac{2π}{3}$,
圆锥的高为$\sqrt{(\sqrt{5})^{2}-1}$=2,
故此圆锥的体积为$\frac{1}{3}$×2×π×12=$\frac{2π}{3}$.
∴此几何体的体积是V=$\frac{2π}{3}+\frac{2π}{3}$=$\frac{4π}{3}$.
故选:A.
点评 本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知i是虚数单位,复数z=a+i(a∈R)满足z2+z=1-3i,则a=( )
| A. | -2 | B. | -2或1 | C. | 2或-1 | D. | 1 |
17.设向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
1.过点P(1,2),并且在两坐标轴上的截距相等的直线方程是( )
| A. | x+y-3=0或x-2y=0 | B. | x+y-3=0或2x-y=0 | ||
| C. | x-y+1=0或x+y-3=0 | D. | x-y+1=0或2x-y=0 |
18.抛物线x=2y2的焦点坐标是( )
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{8}$,0) | D. | (0,$\frac{1}{8}$) |
 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.