题目内容
17.设向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
分析 由条件利用两个向量的数量积的定义求得${\overrightarrow{b}}^{2}$=4,-$\overrightarrow{a}•\overrightarrow{b}$=1,从而求得|2$\overrightarrow{a}$-$\overrightarrow{b}$|的值.
解答 解:∵向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$,且$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,
∴${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$$•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=3=1+2$\overrightarrow{a}$$•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$,且${\overrightarrow{a}}^{2}$=-$\overrightarrow{a}•\overrightarrow{b}$=1,
∴${\overrightarrow{b}}^{2}$=4,-$\overrightarrow{a}•\overrightarrow{b}$=1,∴${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}$$•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=1-2+4=3,
则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{(2\overrightarrow{a}-\overrightarrow{b})}^{2}}$=$\sqrt{{4\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{4+4+4}$=2$\sqrt{3}$,
故选:B.
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{3}{4}$ | B. | $y=-\frac{3}{4}$ | C. | $y=\frac{1}{12}$ | D. | $y=-\frac{1}{12}$ |
| A. | f(x)的图象关于($\frac{π}{12}$,1)中心对称 | B. | f(x)在($\frac{5π}{12}$,$\frac{11π}{12}$)上单调递减 | ||
| C. | f(x)的图象关于x=$\frac{π}{3}$对称 | D. | f(x)的最大值为3 |
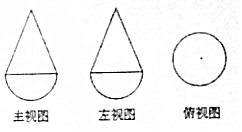 已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | $\frac{10π}{3}$ |
