题目内容
18．抛物线x=2y2的焦点坐标是（ ）| A． | （1，0） | B． | （$\frac{1}{2}$，0） | C． | （$\frac{1}{8}$，0） | D． | （0，$\frac{1}{8}$） |
分析 将抛物线化成标准方程得y2=$\frac{1}{2}$x，根据抛物线的基本概念即可算出该抛物线的焦点坐标．
解答 解：∵抛物线的方程为x=2y2，
∴化成标准方程，得y2=$\frac{1}{2}$x，
由此可得抛物线的2p=$\frac{1}{2}$，得$\frac{p}{2}$=$\frac{1}{8}$
∴抛物线的焦点坐标为（$\frac{1}{8}$，0）
故选C．
点评 本题给出抛物线的方程，求抛物线的焦点坐标，着重考查了抛物线的标准方程与简单几何性质等知识，属于基础题．
练习册系列答案
相关题目
8．已知函数f（x）=$\sqrt{3}$sin2x-cos2x+1，下列结论中错误的是（ ）
| A． | f（x）的图象关于（$\frac{π}{12}$，1）中心对称 | B． | f（x）在（$\frac{5π}{12}$，$\frac{11π}{12}$）上单调递减 | ||
| C． | f（x）的图象关于x=$\frac{π}{3}$对称 | D． | f（x）的最大值为3 |
9．
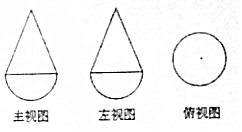已知一个几何体是由上下两部分组成的合体，其三视图如图，若图中圆的半径为1，等腰三角形的腰长为$\sqrt{5}$，则该几何体的体积是（ ）
已知一个几何体是由上下两部分组成的合体，其三视图如图，若图中圆的半径为1，等腰三角形的腰长为$\sqrt{5}$，则该几何体的体积是（ ）| A． | $\frac{4π}{3}$ | B． | 2π | C． | $\frac{8π}{3}$ | D． | $\frac{10π}{3}$ |
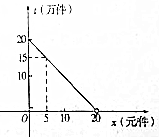2016年9月，第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行，在会展期间某展销商销售一种商品，根据市场调查，每件商品售价x（元）与销量t（万元）之间的函数关系如图所示，又知供货价格与销量呈反比，比例系数为20．（注：每件产品利润=售价-供货价格）
3．若二次函数f（x）=cx2+4x+a（x∈R）的值域为[0，+∞），则$\frac{1}{a}$+$\frac{9}{c}$的最小值为（ ）
| A． | 3 | B． | $\frac{9}{2}$ | C． | 5 | D． | 7 |
