题目内容
19.直线y=2b与双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左支、右支分别交于B,C两点,A为右顶点,O为坐标原点,若∠AOC=∠BOC,则该双曲线的离心率为$\frac{\sqrt{19}}{2}$.分析 利用条件得出∠AOC=60°,C($\frac{2\sqrt{3}}{3}$b,2b),代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{\frac{4}{3}{b}^{2}}{{a}^{2}}$-4=1,b=$\frac{\sqrt{15}}{2}$a,即可得出结论.
解答 解:∵∠AOC=∠BOC,
∴∠AOC=60°,
∴C($\frac{2\sqrt{3}}{3}$b,2b),
代入双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{\frac{4}{3}{b}^{2}}{{a}^{2}}$-4=1,∴b=$\frac{\sqrt{15}}{2}$a,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\frac{\sqrt{19}}{2}$a,
∴e=$\frac{c}{a}$=$\frac{\sqrt{19}}{2}$,
故答案为$\frac{\sqrt{19}}{2}$.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.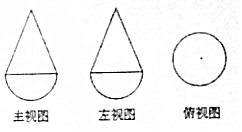 已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
 已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | $\frac{10π}{3}$ |
14.椭圆$\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{11}$=1的焦点坐标为( )
| A. | (±3$\sqrt{2}$,0) | B. | (±2,0) | C. | (0,±3$\sqrt{2}$) | D. | (0,±2) |
4.双曲线$\frac{{x}^{2}}{{2}^{m}+1}$-$\frac{{y}^{2}}{{2}^{-m}+2}$=1的焦距的最小值为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |
11.若函数f(x)=$\frac{sinx}{x+1}$,则f′(0)等于( )
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
