题目内容
14.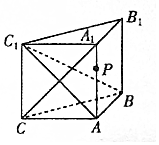 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,AA1+AB+AC=3,AB=AC=t(t>0),P是侧棱AA1上的动点.(1)当AA1=AB=AC时,求证:A1C⊥BC1;
(2)试求三棱锥P-BCC1的体积V取得最大值时的t值.
分析 (1)推导出AC1⊥A1C,AB⊥AC,AB⊥AA1,由此能证明A1C⊥BC1.
(2)推导出点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离,从而三棱锥P-BCC1的体积$V={V}_{P-BC{C}_{1}}$=${V}_{A-BC{C}_{1}}$=${V}_{{C}_{1}-ABC}$,再利用导数能求出三棱锥P-BCC1的体积V取得最大值时的t值.
解答 证明:(1)∵AA1⊥面ABC,∴AA1⊥AC,AA1⊥AB,
又∵AA1=AC,∴四边形AA1C1C是正方形,
∴AC1⊥A1C,
∵AB⊥AC,AB⊥AA1,AA1,AC?平面AA1C1C,AA1∩AC=A,
∴A1C⊥平面ABC1,∴A1C⊥BC1.
解:(2)∵AA1∥平面BB1C1C,
∴点P到平面BB1C1C的距离等于点A到平面BB1C1C的距离,
∴三棱锥P-BCC1的体积:
$V={V}_{P-BC{C}_{1}}$=${V}_{A-BC{C}_{1}}$=${V}_{{C}_{1}-ABC}$=$\frac{1}{6}{t}^{2}(3-2t)$=$\frac{1}{2}{t}^{2}-\frac{1}{3}{t}^{3}$(0<t<$\frac{3}{2}$),
∴V′=-t(t-1),令V′=0,得t=1或t=0(舍),
当t∈(0,1)时,V′>0,函数V(t)是增函数,
当t∈(1,$\frac{3}{2}$)时,V′<0,函数V(t)是减函数,
∴当t=1时,Vmax=$\frac{1}{6}$.
点评 本题考查线线、线面、面面的位置关系等基本知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想等应用意识.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
9.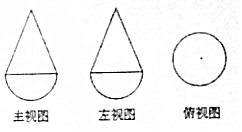 已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
 已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )
已知一个几何体是由上下两部分组成的合体,其三视图如图,若图中圆的半径为1,等腰三角形的腰长为$\sqrt{5}$,则该几何体的体积是( )| A. | $\frac{4π}{3}$ | B. | 2π | C. | $\frac{8π}{3}$ | D. | $\frac{10π}{3}$ |
19.已知直线l1:(m-2)x-y+5=0与l2:(m-2)x+(3-m)y+2=0平行,则实数m的值为( )
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | 4 |
3.若二次函数f(x)=cx2+4x+a(x∈R)的值域为[0,+∞),则$\frac{1}{a}$+$\frac{9}{c}$的最小值为( )
| A. | 3 | B. | $\frac{9}{2}$ | C. | 5 | D. | 7 |
4.双曲线$\frac{{x}^{2}}{{2}^{m}+1}$-$\frac{{y}^{2}}{{2}^{-m}+2}$=1的焦距的最小值为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 5 | D. | 10 |