题目内容
若(2x-1)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),则
+
+
+…+
= .
| 1 |
| 2 |
| a2 |
| 22a1 |
| a3 |
| 23a1 |
| a2014 |
| 22014a1 |
考点:二项式定理的应用
专题:计算题,二项式定理
分析:由题意可得a0=1,通项公式为Tr+1=
•(2x)2014-r•(-1)r,令r=2013,可得a1=-4028,令x=
,可得
+
+…+
=-1,从而可求
+
+
+…+
的值.
| C | r 2014 |
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a2014 |
| 22014 |
| 1 |
| 2 |
| a2 |
| 22a1 |
| a3 |
| 23a1 |
| a2014 |
| 22014a1 |
解答:
解:在(2x-1)2014=a0+a1x+…+a2014x2014 中,显然,a0=1.
通项公式为Tr+1=
•(2x)2014-r•(-1)r,令r=2013,可得a1=-4028
令x=
,可得1+
+
+…+
=0,
∴
+
+…+
=-1,
∴
+
+
+…+
=
.
故答案为:
.
通项公式为Tr+1=
| C | r 2014 |
令x=
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a2014 |
| 22014 |
∴
| a1 |
| 2 |
| a2 |
| 22 |
| a2014 |
| 22014 |
∴
| 1 |
| 2 |
| a2 |
| 22a1 |
| a3 |
| 23a1 |
| a2014 |
| 22014a1 |
| 1 |
| 4028 |
故答案为:
| 1 |
| 4028 |
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题.

练习册系列答案
相关题目
已知动点P(x,y)满足
,动点Q(x,y)在曲线(x-1)2+y2=1上,则|PQ|的最大值与最小值的和为( )
|
A、
| ||||||
B、2
| ||||||
C、
| ||||||
D、3
|
已知函数f(x)的定义域为R,对于定义域内的任意x,满足f(x)=-f(x+1),且当-1<x≤1时,f(x)=1-x2,若函数g(x)=f(x)+x-a恰有两个零点,则实数a的所有可能取值构成的集合为( )
A、{a|a=2k+
| ||||
B、{a|a=2k-
| ||||
C、{a|a=2k+1或2k+
| ||||
| D、{a|a=2k+1,k∈Z} |
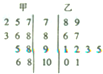 某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.