题目内容
已知函数f(x)的定义域为R,对于定义域内的任意x,满足f(x)=-f(x+1),且当-1<x≤1时,f(x)=1-x2,若函数g(x)=f(x)+x-a恰有两个零点,则实数a的所有可能取值构成的集合为( )
A、{a|a=2k+
| ||||
B、{a|a=2k-
| ||||
C、{a|a=2k+1或2k+
| ||||
| D、{a|a=2k+1,k∈Z} |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:将函数的零点问题转化为两个函数的交点问题,可结合图象进行解题.
解答:
解:∵对于定义域内的任意x,满足f(x)=-f(x+1),
且当-1<x≤1时,f(x)=1-x2,
∴函数f(x)是以2为周期的周期函数,
∵g(x)=f(x)+x-a,
令h(x)=a-x,
∴函数g(x)的零点个数等价于f(x)和h(x)的交点个数,
如图示:
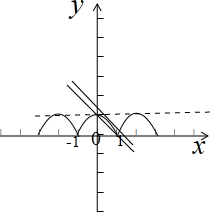 ,
,
∴①h(x)过(1,0)点时与函数f(x)=1-x2有两个交点,
把(1,0)代入h(x)=a-x,解得:a=1,
②函数h(x)与f(x)=1-x2相切时和图象有两个交点,
∴
,
∴x2-x+a-1=0,
△=1-4(a-1)=0,
解得:a=
,
∴a=2k+1,或a=2k+
,k∈Z,
故选:C.
且当-1<x≤1时,f(x)=1-x2,
∴函数f(x)是以2为周期的周期函数,
∵g(x)=f(x)+x-a,
令h(x)=a-x,
∴函数g(x)的零点个数等价于f(x)和h(x)的交点个数,
如图示:
 ,
,∴①h(x)过(1,0)点时与函数f(x)=1-x2有两个交点,
把(1,0)代入h(x)=a-x,解得:a=1,
②函数h(x)与f(x)=1-x2相切时和图象有两个交点,
∴
|
∴x2-x+a-1=0,
△=1-4(a-1)=0,
解得:a=
| 5 |
| 4 |
∴a=2k+1,或a=2k+
| 5 |
| 4 |
故选:C.
点评:本题考察了函数的零点问题,渗透了数形结合思想,考察了周期函数,是一道中档题.

练习册系列答案
相关题目
已知x,y满足不等式组
,则目标函数z=2x+y的最大值为( )
|
| A、5 | B、6 | C、7 | D、8 |
设m∈R,则m=1是直线l1:(m+1)x+2y-1=0和l2:x+my+4=0平行的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分又不必要条件 |
 执行如图所示的程序框图,若输出b的值为15,则图中判断框内①处应填的数是( )
执行如图所示的程序框图,若输出b的值为15,则图中判断框内①处应填的数是( )| A、2 | B、3 | C、4 | D、5 |
已知双曲线
-
=1(a>0,b>0),A1、A2是双曲线的顶点,F是右焦点,点B(0,b),若在线段BF上(不含端点)存在不同的两点Pi(i=1,2),使得△PiA1A2(i=1,2)构成以线段A1A2为斜边的直角三角形,则双曲线离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||||||
B、(
| ||||||
C、(1,
| ||||||
D、(
|
向量
=(-3,4),
=-2
,若A点的坐标是(1,2),则B点的坐标为( )
| a |
| AB |
| a |
| A、(-7,8) |
| B、(7,-6) |
| C、(-5,10) |
| D、(9,-4) |
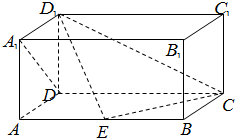 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.