题目内容
某商店销售洗衣粉,年销售总量为6000包,每包进价2.8元,销售价3.4元.全年分若干次进货,每次进货均为x包.已知每次进货运输劳务费为62.5元,全年保管费为1.5x元.
(1)把该店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大化,问每次该进货多少包?
(1)把该店经销洗衣粉一年的利润y(元)表示为每次进货量x(包)的函数,并指出函数的定义域;
(2)为了使利润最大化,问每次该进货多少包?
考点:函数最值的应用
专题:应用题,函数的性质及应用,不等式的解法及应用
分析:(1)由年销售总量为6000包,每次进货均为x包,可得进货次数,进而根据每包进价为2.8元,销售价为3.4元,计算出收入,由每次进货的运输劳务费为62.5元,全年保管费为1.5x元计算出成本,相减可得利润的表达式;
(2)由(1)中函数的解析式,由基本不等式,结合x的实际意义,可得使利润最大,每次应进货包数.
(2)由(1)中函数的解析式,由基本不等式,结合x的实际意义,可得使利润最大,每次应进货包数.
解答:
解:(1)由题意可知:一年总共需要进货
(x∈N*且x≤6000)次,
∴y=3.4×6000-2.8×6000-
•62.5-1.5x,
整理得:y=3600-
-
(x∈N*且x≤6000).
(2)y=3600-
-
≤3600-2
=2100
(当且仅当
=
,即x=500时取等号)
∴当x=500时,ymax=3600-1500=2100(元),
答:当每次进货500包时,利润最大为2100元.
| 6000 |
| x |
∴y=3.4×6000-2.8×6000-
| 6000 |
| x |
整理得:y=3600-
| 37500 |
| x |
| 3x |
| 2 |
(2)y=3600-
| 37500 |
| x |
| 3x |
| 2 |
|
(当且仅当
| 37500 |
| x |
| 3x |
| 2 |
∴当x=500时,ymax=3600-1500=2100(元),
答:当每次进货500包时,利润最大为2100元.
点评:本题考查的知识点是函数最值的应用,其中根据已知条件计算出利润y(元)元表示为每次进货量x(包)的函数表达式是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=Acos(ωx+φ)的图象如图所示,f(
)=-
,则f(-
)=( )

| π |
| 2 |
| 2 |
| 3 |
| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知a是空间任意一条直线,α是一个平面,则平面α内一定存在直线与直线a( )
| A、相交 | B、平行 | C、异面 | D、垂直 |
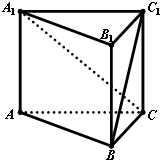 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<