题目内容
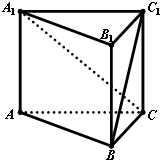 在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;
(2)是否存在过A1C的平面α,使得直线BC1∥α平行,若存在请作出平面α并证明,若不存在请说明理由.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:作图题,证明题,空间位置关系与距离
分析:(1)由矩形由找到垂直,证明AA1⊥平面ABC;从而证明BC⊥平面ACC1A1.
(2)先说明存在,然后作图证明;连接A1C,AC1,设A1C∩AC1=D,取线段AB的中点M,连接A1M,MC.则平面A1CM为为所求的平面α.
(2)先说明存在,然后作图证明;连接A1C,AC1,设A1C∩AC1=D,取线段AB的中点M,连接A1M,MC.则平面A1CM为为所求的平面α.
解答:
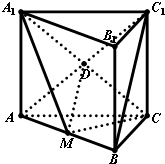 解:(1)证明:∵四边形ABB1A1和ACC1A1都是矩形,
解:(1)证明:∵四边形ABB1A1和ACC1A1都是矩形,
∴AA1⊥AB,AA1⊥AC,
∵AB,AC为平面ABC内的两条相交直线,
∴AA1⊥平面ABC;
∵直线BC?平面ABC,
∴AA1⊥BC
又由已知,AC⊥BC,AA1,AC为平面ACC1A1内的两条相交直线,
∴BC⊥平面ACC1A1.
(2)存在,证明如下:
连接A1C,AC1,设A1C∩AC1=D,取线段AB的中点M,连接A1M,MC.
则平面A1CM为为所求的平面α.
由作图可知M,D分别为AB、AC1的中点,
∴MD
BC1,
又∵MD?α,BC1?α
∴BC1∥α.
 解:(1)证明:∵四边形ABB1A1和ACC1A1都是矩形,
解:(1)证明:∵四边形ABB1A1和ACC1A1都是矩形,∴AA1⊥AB,AA1⊥AC,
∵AB,AC为平面ABC内的两条相交直线,
∴AA1⊥平面ABC;
∵直线BC?平面ABC,
∴AA1⊥BC
又由已知,AC⊥BC,AA1,AC为平面ACC1A1内的两条相交直线,
∴BC⊥平面ACC1A1.
(2)存在,证明如下:
连接A1C,AC1,设A1C∩AC1=D,取线段AB的中点M,连接A1M,MC.
则平面A1CM为为所求的平面α.
由作图可知M,D分别为AB、AC1的中点,
∴MD
| ||
. |
| 1 |
| 2 |
又∵MD?α,BC1?α
∴BC1∥α.
点评:本题考查了线面垂直的判定定理与性质,同时考查了作图方法,属于中档题.

练习册系列答案
相关题目
若实数x,y满足条件
目标函数z=2x-y,则( )
|
A、zmax=
| ||
| B、zmax=0 | ||
| C、zmax=-1 | ||
| D、zmax=2 |
设命题p:|2x-3|<1,q:
≤0,则p是q的( )
| x-3 |
| x-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |