题目内容
已知椭圆的短轴为2
,左、右焦点分别为F1、F2,点P在椭圆上,且满足△PF1F2的周长为6.
(1)求椭圆的标准方程;
(2)若直线l与椭圆交于A、B两点,△ABO面积为
,判断|OA|2+|OB|2是否为定值?若为定值,求出定值;若不为定值,说明理由.
| 3 |
(1)求椭圆的标准方程;
(2)若直线l与椭圆交于A、B两点,△ABO面积为
| 3 |
考点:直线与圆锥曲线的综合问题
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)运用待定系数法,设出椭圆方程,由题意得,2b=2
,2a+2c=6,又a2=b2+c2,解出a,b即可;
(2)设直线l:y=kx+m,联立椭圆方程和直线方程,消去y,运用韦达定理,弦长公式和三角形的面积公式,化简整理,得到3+4k2=2m2,再由|OA|2+|OB|2=x12+x22+y12+y22代入化简整理,即可得到为定值.
| 3 |
(2)设直线l:y=kx+m,联立椭圆方程和直线方程,消去y,运用韦达定理,弦长公式和三角形的面积公式,化简整理,得到3+4k2=2m2,再由|OA|2+|OB|2=x12+x22+y12+y22代入化简整理,即可得到为定值.
解答:
解:(1)设椭圆的标准方程为:
+
=1.
由椭圆的短轴为2
,即有2b=2
,
由于△PF1F2的周长为6,则2a+2c=6,
又a2=b2+c2,
解得a=2,b=
,c=1,
∴椭圆C方程为:
+
=1;
(2)设直线l:y=kx+m,联立椭圆方程,消去y,
得到:(3+4k2)x2+8kmx+4m2-12=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
,
判别式△=64k2m2-4(3+4k2)(4m2-12)>0,
即3+4k2>m2,
点O到直线的距离d=
,
弦长AB=
|x1-x2|,
则△ABC面积为S=
d•|AB|=
•|x1-x2|•
=
,
即有m2(
-
)=12,化简得,(3+4k2)2-4(3+4k2)m2+4m4=0,
即为(3+4k2-2m2)2=0,即3+4k2=2m2,检验判别式大于0,
则k2=
,x1+x2=
,x1x2=2-
,
则|OA|2+|OB|2=x12+x22+y12+y22=(1+k2)[(x1+x2)2-2x1x2]+2km(x1+x2)+2m2
=(1+
)[
-2(2-
)]-
+2m2
=2m2+1-4m2+6+2m2=7.
故|OA|2+|OB|2为定值,且为7.
| x2 |
| a2 |
| y2 |
| b2 |
由椭圆的短轴为2
| 3 |
| 3 |
由于△PF1F2的周长为6,则2a+2c=6,
又a2=b2+c2,
解得a=2,b=
| 3 |
∴椭圆C方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)设直线l:y=kx+m,联立椭圆方程,消去y,
得到:(3+4k2)x2+8kmx+4m2-12=0,
设A(x1,y1),B(x2,y2),
则x1+x2=
| -8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
判别式△=64k2m2-4(3+4k2)(4m2-12)>0,
即3+4k2>m2,
点O到直线的距离d=
| |m| | ||
|
弦长AB=
| 1+k2 |
则△ABC面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1+k2 |
| |m| | ||
|
| 3 |
即有m2(
| 64k2m2 |
| (3+4k2)2 |
| 16m2-48 |
| 3+4k2 |
即为(3+4k2-2m2)2=0,即3+4k2=2m2,检验判别式大于0,
则k2=
| 2m2-3 |
| 4 |
| -4k |
| m |
| 6 |
| m2 |
则|OA|2+|OB|2=x12+x22+y12+y22=(1+k2)[(x1+x2)2-2x1x2]+2km(x1+x2)+2m2
=(1+
| 2m2-3 |
| 4 |
16•
| ||
| m2 |
| 6 |
| m2 |
16×
| ||
| 2m2 |
=2m2+1-4m2+6+2m2=7.
故|OA|2+|OB|2为定值,且为7.
点评:本题考查椭圆的方程和性质及运用,考查联立直线方程和椭圆方程,消去未知数,运用韦达定理,弦长公式,和面积公式,考查化简和整理的运算求解能力,具有一定的运算量,属于综合题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
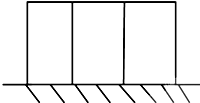 用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y
用长度为20m的篱笆围建一个一面靠墙的矩形鸡舍,且鸡舍内用相同的篱笆隔成三间(如图所示),如果挨着墙的边长为x,鸡舍面积为y(1)请把y表示成x的函数;
(2)当x为何值时,函数取最大值,并求出最大值.
若ab>0,则下列四个等式:
①lg(ab)=lga+lgb
②lg(
)=lga-lgb
③
lg(
)2=lg(
)
④lg(ab)=
中正确等式的符号是( )
①lg(ab)=lga+lgb
②lg(
| a |
| b |
③
| 1 |
| 2 |
| a |
| b |
| a |
| b |
④lg(ab)=
| 1 |
| logab10 |
| A、①②③④ | B、①② | C、③④ | D、③ |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、“x=-1”是“x2-2x-3=0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x-1<0”的否定是“?x∈R,均有x2+x-1>0” |
| D、命题“已知x,y∈R,若x+y≠5,则x≠1或y≠4”为真命题 |
已知数列{an}为等差数列,Sn是数列{an}的前n项和,a1+a6+a11=4π,则sin(S11)的值为( )
A、
| ||||
B、±
| ||||
C、
| ||||
D、-
|
