题目内容
已知“k∈(m,+∞)”是“
+
≥
”的充分不必要条件,则实数的取值范围是 .
| x2 |
| 2 |
| y2 |
| 8 |
| xy |
| 2k |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:由原不等式想着求k的范围,这需要不等式两边同除以
+
,所以讨论
+
是否为0.为0时不可同除以该式,此时x=y=0,显然原不等式对任意的k都成立,并且此时的m∈R;当
+
≠0,即x,y不同时为0,可以得到:2k≥
,根据基本不等式
+
≥2•
•
=
,所以得到
≤2,所以2k≥2,k≥1,所以此时m应满足:m≥1,这样便得到实数m的取值范围了.
| x2 |
| 2 |
| y2 |
| 8 |
| x2 |
| 2 |
| y2 |
| 8 |
| x2 |
| 2 |
| y2 |
| 8 |
| xy | ||||
|
| x2 |
| 2 |
| y2 |
| 8 |
| x | ||
|
| y | ||
|
| xy |
| 2 |
| xy | ||||
|
解答:
解:x=y=0时,原不等式对于任意的k∈R都成立,并且满足k∈(m,+∞)是
+
≥
的充分不必要条件,此时m∈R;
x,y不同时为0时,
+
>0,∴由原不等式得2k≥
;
∵
+
≥2•
•
=
;
∴
≤2;
∴2k≥2,k≥1;
∵k∈(m,+∞)是
+
≥
的充分不必要条件,∴m≥1;
综上得实数m的取值范围是[1,+∞).
故答案为:[1,+∞).
| x2 |
| 2 |
| y2 |
| 8 |
| xy |
| 2k |
x,y不同时为0时,
| x2 |
| 2 |
| y2 |
| 8 |
| xy | ||||
|
∵
| x2 |
| 2 |
| y2 |
| 8 |
| x | ||
|
| y | ||
|
| xy |
| 2 |
∴
| xy | ||||
|
∴2k≥2,k≥1;
∵k∈(m,+∞)是
| x2 |
| 2 |
| y2 |
| 8 |
| xy |
| 2k |
综上得实数m的取值范围是[1,+∞).
故答案为:[1,+∞).
点评:考查充分条件、必要条件、充分不必要条件的概念,指数函数的单调性,以及基本不等式:a2+b2≥2ab.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
已知集合A={0,1},B={x∈R|0<x<2},则A∩B=( )
| A、{0} | B、{1} |
| C、[0,1] | D、(0,1) |
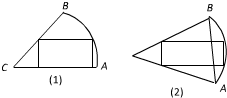 某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.
某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.