题目内容
11.“a=-1”是“直线ax+3y+3=0与直线x+(a-2)y-3=0平行”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据直线平行的等价条件求出a的值,结合充分条件和必要条件的定义进行判断即可.
解答 解:当a=-1时,两直线方程为-x+3y+3=0和x-3y-3=0,此时两直线重合,不满足条件.
若直线ax+3y+3=0与直线x+(a-2)y-3=0平行,
若a=0时,两直线方程为3y+3=0和x-2y-3=0,此时两直线相交,不满足条件.
若a≠0,若两直线平行,则$\frac{1}{a}=\frac{a-2}{3}$$≠\frac{-3}{3}$,
由$\frac{1}{a}=\frac{a-2}{3}$得a(a-2)=3,即a2-2a-3=0,得a=-1或a=3,
当a=-1时,两直线重合,∴a=3,
则“a=-1”是“直线ax+3y+3=0与直线x+(a-2)y-3=0平行”的既不充分也不必要条件,
故选:D
点评 本题主要考查充分条件和必要条件的判断,根据直线平行的等价条件求出a的值是解决本题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
2.已知全集U=R,集合$A=\left\{{y\left|{y={{(\frac{1}{2})}^x}+1}\right.}\right\}$,集合B={y|y=b,b∈R},若A∩B=∅,则b的取值范围是( )
| A. | b<0 | B. | b≤0 | C. | b<1 | D. | b≤1 |
19.已知△ABC中,BC=1,A=120°,∠B=θ,记f(θ)=$\overrightarrow{BC}•\overrightarrow{AC}$,
①求f(θ)关于θ的表达式.
②求f(θ)的值域.
①求f(θ)关于θ的表达式.
②求f(θ)的值域.
16.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | $\frac{2π}{3}$ | B. | π | C. | 2π | D. | 3π |
3.已知梯形ABCD中,∠ABC=∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,P是DC的中点,则|$\overrightarrow{PA}$+2$\overrightarrow{PB}$|=( )
| A. | $\frac{\sqrt{82}}{2}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 5 |
20.当实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$时,目标函数z=ax+y的最大值为3,则实数a的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
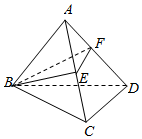 如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.
如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.