题目内容
20.当实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$时,目标函数z=ax+y的最大值为3,则实数a的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
分析 画出约束条件表示的可行域,判断目标函数z=ax+y取得最大值的位置,求出a即可.
解答  解:作出实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$的可行域如图:
解:作出实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ 2x+y≤2\end{array}\right.$的可行域如图:
目标函数z=ax+y的最大值为3,就是直线z=ax+y经过(0,3)点,可知a>0,目标函数的最优解是A,由$\left\{\begin{array}{l}{2x+y=2}\\{y=0}\end{array}\right.$解得A(1,0)
目标函数在A(1,0)处取最大值3,2a=3.
解得a=$\frac{3}{2}$
故选:B.
点评 本题考查简单的线性规划的应用,正确画出可行域,判断目标函数经过的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.“a=-1”是“直线ax+3y+3=0与直线x+(a-2)y-3=0平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.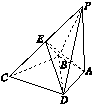 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
(1)求证:AB⊥BC;
(2)若PA=$\sqrt{3}$,E为PC的中点,求三棱锥EABD的体积.
 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.(1)求证:AB⊥BC;
(2)若PA=$\sqrt{3}$,E为PC的中点,求三棱锥EABD的体积.
10.已知α为第三象限角,化简cosα$\sqrt{\frac{1+sinα}{1-sinα}}$-sinα$\sqrt{\frac{1+cosα}{1-cosα}}$得( )
| A. | cosα-sinα | B. | sinα+cosα+2 | C. | sinα-cosα | D. | -sinα-cosα-2 |
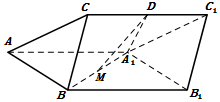 如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.
如图,三棱柱ABC-A1B1C1中,侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$,D,M分别为CC1和A1B的中点,A1D⊥CC1,AA1=A1D=2,BC=1.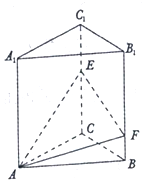 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.