题目内容

1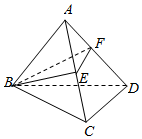．如图，在三棱锥A-BCD中，E是AC中点，F在线段AD上，且FD=3AF，则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$．

分析 利用三角形的面积公式计算出△AEF与△ACD的面积比，从而得出他们的体积比．

解答 解：∵FD=3AF，∴AF=$\frac{1}{4}$AD，
∴S△AEF=$\frac{1}{2}$AE•AF•sin∠CAD=$\frac{1}{2}$•$\frac{1}{2}$AC•$\frac{1}{4}$AD•sin∠CAD=$\frac{1}{8}$S△ACD，
∴S△AEF：S四边形EFDC=1：7，
∴VB-AEF：VB-EFDC=S△AEF：S四边形EFDC=1：7，
故答案为：$\frac{1}{7}$．

点评 本题考查了棱锥的体积计算公式，属于中档题．

练习册系列答案
相关题目
18．在钝角△ABC中，角A，B，C所对的边分别为a，b，c且b=atanB．
（Ⅰ）求A-B的值；
（Ⅱ）求cos2B-sinA的取值范围．
12．已知向量$\overrightarrow a$和$\overrightarrow b$的夹角为120°，且$|\overrightarrow a|=2，|\overrightarrow b|=1$．
（1）求$（2\overrightarrow a-\overrightarrow b）•\overrightarrow a$的值；
（2）求$|\overrightarrow a+2\overrightarrow b|$的值．
9．已知f'（x）是奇函数f（x）的导函数，f（-1）=0，当x＞0时，f′（x）＜$\frac{f（x）}{x}$，则使得f（x）＞0成立的x的取值范围是（　　）
A．（-∞，-1）∪（0，1）B．（-1，0）∪（1，+∞）C．（-1，0）∪（0，1）D．（-∞，-1）∪（1，+∞）
16．设实数x，y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}\right.$，则z=$\frac{4x}{y}$+$\frac{y}{x}$的取值范围是（　　）
A．[4，$\frac{17}{2}$]B．[$\frac{13}{3}$，$\frac{17}{2}$]C．[4，$\frac{37}{3}$]D．[$\frac{17}{2}$，$\frac{37}{3}$]
6．已知$\overrightarrow m=（cos\frac{x}{2}，sin\frac{x}{2}）$，$\overrightarrow n=（-\sqrt{3}，1）$，则$|\overrightarrow m-\overrightarrow n|$的最大值是3．
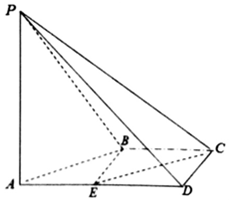13．如图，在四棱锥P-ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD=$\frac{1}{2}$AD，E为AD的中点，异面直线AP与CD所成的角为90°．
（Ⅰ）证明：△PBE是直角三角形；
（Ⅱ）若二面角P-CD-A的大小为45°，求二面角A-PE-C的余弦值．
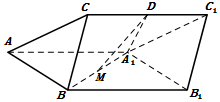10．如图，三棱柱ABC-A1B1C1中，侧面ABB1A1为菱形且$∠BA{A_1}={60^o}$，D，M分别为CC1和A1B的中点，A1D⊥CC1，AA1=A1D=2，BC=1．
（Ⅰ）证明：直线MD∥平面ABC；
（Ⅱ）求二面角B-AC-A1的余弦值．
11．“a=-1”是“直线ax+3y+3=0与直线x+（a-2）y-3=0平行”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网