题目内容
6.已知菱形ABCD的边长为4,∠BAD=150°,点E,F分别在边BC,CD上,2CE=3EB,DC=λDF(λ∈R,λ≠0),若$\overrightarrow{AE}•\overrightarrow{AF}=\frac{42}{5}({1-\sqrt{3}})$,则λ的值为8.分析 用$\overrightarrow{AB}$,$\overrightarrow{AD}$表示出$\overrightarrow{AE}$,$\overrightarrow{AF}$,根据数量积列方程解出λ.
解答  解:∵2CE=3EB,∴$\overrightarrow{BE}$=$\frac{2}{5}$$\overrightarrow{BC}$=$\frac{2}{5}$$\overrightarrow{AD}$,
解:∵2CE=3EB,∴$\overrightarrow{BE}$=$\frac{2}{5}$$\overrightarrow{BC}$=$\frac{2}{5}$$\overrightarrow{AD}$,
∴$\overrightarrow{AE}$=$\overrightarrow{AB}+\overrightarrow{BE}$=$\overrightarrow{AB}+$$\frac{2}{5}\overrightarrow{AD}$,
∵DC=λDF,∴$\overrightarrow{DF}$=$\frac{1}{λ}$$\overrightarrow{DC}$=$\frac{1}{λ}$$\overrightarrow{AB}$,
∴$\overrightarrow{AF}$=$\overrightarrow{AD}+\overrightarrow{DF}$=$\frac{1}{λ}$$\overrightarrow{AB}$+$\overrightarrow{AD}$,
∴$\overrightarrow{AE}•\overrightarrow{AF}$=($\overrightarrow{AB}+$$\frac{2}{5}\overrightarrow{AD}$)•($\frac{1}{λ}$$\overrightarrow{AB}$+$\overrightarrow{AD}$)=$\frac{1}{λ}$${\overrightarrow{AB}}^{2}$+(1+$\frac{2}{5λ}$)$\overrightarrow{AB}•\overrightarrow{AD}$+$\frac{2}{5}$$\overrightarrow{AD}$2,
∵菱形ABCD的边长为4,∠BAD=150°,
∴${\overrightarrow{AB}}^{2}$=${\overrightarrow{AD}}^{2}$=16,$\overrightarrow{AB}•\overrightarrow{AD}$=4×4×cos150°=-8$\sqrt{3}$,
∵$\overrightarrow{AE}•\overrightarrow{AF}$=$\frac{16}{λ}$+(1+$\frac{2}{5λ}$)•(-8$\sqrt{3}$)+$\frac{32}{5}$=$\frac{42}{5}$(1-$\sqrt{3}$),
解得λ=8.
故答案为:8.
点评 本题考查了平面向量在几何中的应用,平面向量的数量积运算,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | [4,$\frac{17}{2}$] | B. | [$\frac{13}{3}$,$\frac{17}{2}$] | C. | [4,$\frac{37}{3}$] | D. | [$\frac{17}{2}$,$\frac{37}{3}$] |
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | ∠MCN<θ | B. | ∠MCN=θ | ||
| C. | ∠MCN>θ | D. | 以上三种情况都有可能 |
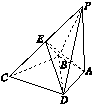 如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.
如图所示,PA与四边形ABCD所在平面垂直,且PA=BC=CD=BD,AB=AD,PD⊥DC.(1)求证:AB⊥BC;
(2)若PA=$\sqrt{3}$,E为PC的中点,求三棱锥EABD的体积.
| A. | -6 | B. | -1 | C. | 1 | D. | 6 |
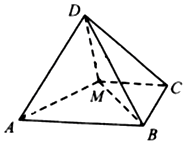 如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.