题目内容
已知函数f(x)=|x2+x-2|,x∈R.若方程f(x)-a|x-2|=0恰有4个互异的实数根,则实数a的取值范围为 .
考点:根的存在性及根的个数判断
专题:计算题,数形结合,函数的性质及应用
分析:由y=f(x)-a|x-2|=0得f(x)=a|x-2|,显然x=2不是方程的根,则a=|
|,令x-2=t,则a=|t+
+5|有4个不相等的实根,画出y=|t+
+5|的图象,利用数形结合即可得到结论.
| x2+x-2 |
| x-2 |
| 4 |
| t |
| 4 |
| t |
解答:
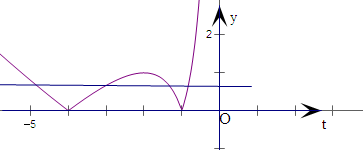 解:方程f(x)-a|x-2|=0,
解:方程f(x)-a|x-2|=0,
即为f(x)=a|x-2|,
即有|x2+x-2|=a|x-2|,
显然x=2不是方程的根,
则a=|
|,
令x-2=t,则a=|t+
+5|有4个不相等的实根,画出y=|t+
+5|(t<0)的图象,如右图:
在-4<t<-1时,t+
+5≤-2
+5=1.
在x>2时,t+
+5>9,
则要使直线y=a和y=|t+
+5|的图象有四个交点,则a的范围是(0,1)∪(9,+∞),
故答案为(0,1)∪(9,+∞).
 解:方程f(x)-a|x-2|=0,
解:方程f(x)-a|x-2|=0,即为f(x)=a|x-2|,
即有|x2+x-2|=a|x-2|,
显然x=2不是方程的根,
则a=|
| x2+x-2 |
| x-2 |
令x-2=t,则a=|t+
| 4 |
| t |
| 4 |
| t |
在-4<t<-1时,t+
| 4 |
| t |
t•
|
在x>2时,t+
| 4 |
| t |
则要使直线y=a和y=|t+
| 4 |
| t |
故答案为(0,1)∪(9,+∞).
点评:本题主要考查函数零点个数的应用,利用数形结合是解决本题的关键,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图,输出s的值等于( )


| A、98 | B、100 |
| C、2450 | D、2550 |
如图是一个算法的程序框图,当输入的x值为5时,输出y的结果恰好是
,则①处的关系式是( )

| 1 |
| 3 |

A、y=x
| ||
| B、y=x-3 | ||
| C、y=3x | ||
| D、y=x3 |
已知全集U=R,集合A={x||x|<3},B={x|x-2≥0},则A∪∁UB等于( )
| A、(-∞,3] |
| B、(-∞,3) |
| C、[2,3) |
| D、(-3,2] |
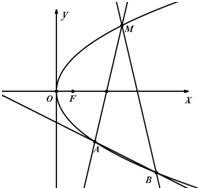 已知点F为抛物线C:y2=2px(p>0)的焦点,M(4,t)(t>0)为抛物线C上的点,且|MF|=5.
已知点F为抛物线C:y2=2px(p>0)的焦点,M(4,t)(t>0)为抛物线C上的点,且|MF|=5. 假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域,则称这条直线平分这个区域.如图,?是平面α内的任意一个封闭区域.现给出如下结论:
假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域,则称这条直线平分这个区域.如图,?是平面α内的任意一个封闭区域.现给出如下结论: