题目内容
如图,矩形ABCD中,AB=2AD=2,点p在以AB为直径的半圆上移动,若
=λ
,则λ+μ的最大值是( )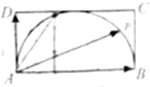
| AP |
| AD |

A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
考点:平面向量数量积的运算
专题:计算题,三角函数的求值,平面向量及应用
分析:以A为坐标原点,AB,AD所在直线为x,y轴建立坐标系,分别求得A,B,D,设∠PAB=α(0≤α≤
),求得P的坐标,再由已知条件得到λ+μ=
+
,运用两角和的正弦公式,化简结合正弦函数的值域即可得到最大值.
| π |
| 2 |
| 1 |
| 2 |
| 2sin2α+cos2α |
| 2 |
解答:
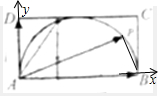 解:以A为坐标原点,AB,AD所在直线为x,y轴建立坐标系,
解:以A为坐标原点,AB,AD所在直线为x,y轴建立坐标系,
则B(2,0),D(0,1),A(0,0),
=(2,0),
=(0,1),
设∠PAB=α(0≤α≤
),
则P(2cosαcosα,2cosαsinα)即为
=(1+cos2α,sin2α),
由
=λ
+μ
,可得,
λ=
,μ=sin2α,
即有λ+μ=
+
=
+
sin(2α+θ),(tanθ=
,θ为锐角),
当且仅当2α+θ=
时,取得最大值,且为
.
故选D.
 解:以A为坐标原点,AB,AD所在直线为x,y轴建立坐标系,
解:以A为坐标原点,AB,AD所在直线为x,y轴建立坐标系,则B(2,0),D(0,1),A(0,0),
| AB |
| AD |
设∠PAB=α(0≤α≤
| π |
| 2 |
则P(2cosαcosα,2cosαsinα)即为
| AP |
由
| AP |
| AB |
| AD |
λ=
| 1+cos2α |
| 2 |
即有λ+μ=
| 1 |
| 2 |
| 2sin2α+cos2α |
| 2 |
=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
当且仅当2α+θ=
| π |
| 2 |
1+
| ||
| 2 |
故选D.
点评:本题考查平面向量的坐标表示,考查三角函数的化简和求值,考察正弦函数的性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0<x<1,都有f(x)=lnx+
,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 1 |
| x |
| 2009 |
| 4 |
| 2011 |
| 2 |
| 2013 |
| 5 |
| A、c<a<b |
| B、a<c<b |
| C、c<b<a |
| D、a<b<c |
 如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图,现已知年龄 在[30,35),[35,40),[40,45]的上网人数呈现递减的等差数列,则年龄在[35,40)的频( )
如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图,现已知年龄 在[30,35),[35,40),[40,45]的上网人数呈现递减的等差数列,则年龄在[35,40)的频( )| A、0.04 | B、0.06 |
| C、0.2 | D、0.3 |
解决某一问题而设计的 ( ) 有限的步骤称为算法.
| A、确定的 | B、有效的 |
| C、连续的 | D、无穷的 |
 已知直线l过点P(3,2).
已知直线l过点P(3,2).