题目内容
若函数y=x2+2ax+1在（-∞，5]上是减函数，则实数a的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：求函数y=x2+2ax+1的对称轴，根据二次函数的单调性即可求出a的取值范围．
解答：
解：原函数的对称轴为x=-a；
∵该函数在（-∞，5]上是减函数；
∴-a≥5，a≤-5；
∴实数a的取值范围是（-∞，-5]．
故答案为：（-∞，-5]．
∵该函数在（-∞，5]上是减函数；
∴-a≥5，a≤-5；
∴实数a的取值范围是（-∞，-5]．
故答案为：（-∞，-5]．
点评：考查二次函数的对称轴，以及二次函数的单调性．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
化简：
的结果是（ ）
| sin2(α+π)•cos(π+α) |
| cos3(-α-π)•tan2(α-2π) |
| A、1 | ||
| B、-1 | ||
| C、cosα | ||
D、
|
如图，矩形ABCD中，AB=2AD=2，点p在以AB为直径的半圆上移动，若
=λ
，则λ+μ的最大值是（ ）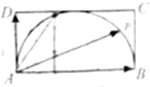
| AP |
| AD |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|