题目内容
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0<x<1,都有f(x)=lnx+
,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 1 |
| x |
| 2009 |
| 4 |
| 2011 |
| 2 |
| 2013 |
| 5 |
| A、c<a<b |
| B、a<c<b |
| C、c<b<a |
| D、a<b<c |
考点:函数奇偶性的性质
专题:函数的性质及应用,导数的综合应用
分析:根据已知条件即可得到f(x)=(-1)nf(x-2n),n∈N*,所以可求得a=-f(
),b=-f(
),c=-f(
),而通过求导能够判断f(x)在(0,1)上单调递减,从而可比较f(
),f(
),f(
)的大小关系,从而得出a,b,c的大小关系.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 5 |
解答:
解:根据已知条件,f(x)=f(x-1+1)=-f[-(x-1)+1]=-f(x-2)=(-1)nf(x-2n),n∈N*;
∴a=f(
)=f(
+502)=(-1)251f(
+502-2×251)=-f(
);
b=f(
+1005)=f(
+1+2×502)=f(
+1)=-f(
);
c=f(
+402)=-f(
);
0<x<1时,f′(x)=
-
=
<0;
∴f(x)在(0,1)上是减函数;
∴f(
)<f(
)<f(
);
∴-f(
)>-f(
)>-f(
);
即a<b<c.
故选:D.
∴a=f(
| 2009 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
b=f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
c=f(
| 3 |
| 5 |
| 3 |
| 5 |
0<x<1时,f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
∴f(x)在(0,1)上是减函数;
∴f(
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 4 |
∴-f(
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 4 |
即a<b<c.
故选:D.
点评:考查奇函数,偶函数的定义,以及通过判断导数符号判断函数单调性的方法,根据函数单调性比较函数值的大小.

练习册系列答案
相关题目
化简:
的结果是( )
| sin2(α+π)•cos(π+α) |
| cos3(-α-π)•tan2(α-2π) |
| A、1 | ||
| B、-1 | ||
| C、cosα | ||
D、
|
如图,矩形ABCD中,AB=2AD=2,点p在以AB为直径的半圆上移动,若
=λ
,则λ+μ的最大值是( )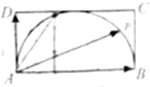
| AP |
| AD |

A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
从一个不透明的口袋中找出红球的概率为
,已知袋中红球有3个,则袋中共有球的个数为( )
| 1 |
| 5 |
| A、5个 | B、8个 |
| C、10个 | D、15个 |