题目内容
已知x>0,y>0,x+y=1,n∈N*,求证:x2n+y2n≥
.
| 1 |
| 22n-1 |
考点:不等式的证明
专题:推理和证明
分析:构造f(x)=x2n+(1-x)2n-
,利用导数法可求得f(x)min=f(
)=0,从而可得f(x)≥0,即所证的不等式成立.
| 1 |
| 22n-1 |
| 1 |
| 2 |
解答:
证明:因为x>0,y>0,x+y=1,n∈N*,
所以,y=1-x∈(0,1),同理知,x∈(0,1).
构造函数f(x)=x2n+(1-x)2n-
,下面只需证明f(x)≥0.
则f′(x)=2n[x2n-1-(1-x)2n-1],
令f′(x)=0,则x2n-1=(1-x)2n-1,解得x=
,
当1>x>
时,x2n-1>(1-x)2n-1,故f′(x)>0;
当0<x<
时,x2n-1<(1-x)2n-1,故f′(x)<0;
所以x=
为f(x)=0的唯一极小值点,
所以f(x)≥f(x)min=f(
)=(
)2n+(
)2n-
=(
)2n-1-(
)2n-1=0,
所以,x2n+y2n≥
,即待证式成立.
所以,y=1-x∈(0,1),同理知,x∈(0,1).
构造函数f(x)=x2n+(1-x)2n-
| 1 |
| 22n-1 |
则f′(x)=2n[x2n-1-(1-x)2n-1],
令f′(x)=0,则x2n-1=(1-x)2n-1,解得x=
| 1 |
| 2 |
当1>x>
| 1 |
| 2 |
当0<x<
| 1 |
| 2 |
所以x=
| 1 |
| 2 |
所以f(x)≥f(x)min=f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
所以,x2n+y2n≥
| 1 |
| 22n-1 |
点评:本题考查不等式的证明,构造函数f(x)=x2n+(1-x)2n-
,利用导数法可求得f(x)min=f(
)=0是关键,也是难点,考查创新思维与推理论证能力,属于难题.
| 1 |
| 22n-1 |
| 1 |
| 2 |

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
化简:
的结果是( )
| sin2(α+π)•cos(π+α) |
| cos3(-α-π)•tan2(α-2π) |
| A、1 | ||
| B、-1 | ||
| C、cosα | ||
D、
|
如图,矩形ABCD中,AB=2AD=2,点p在以AB为直径的半圆上移动,若
=λ
,则λ+μ的最大值是( )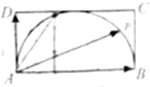
| AP |
| AD |

A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
“x∈{a,3}”是不等式2x2-5x-3≥0成立的一个充分不必要条件,则实数a的取值范围是( )
| A、(3,+∞) | ||
B、(-∞,-
| ||
C、(-∞,-
| ||
D、(-∞,-
|