题目内容
 已知直线l过点P(3,2).
已知直线l过点P(3,2).(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l与x轴、y轴的正半轴分别交于A、B两点,如图所示,求△ABO的面积的最小值及此时直线l的方程.
考点:直线的截距式方程
专题:直线与圆
分析:(1)当直线经过原点时,可得直线方程为y=
x.当直线不经过原点时,可设直线方程为x+y=a,把点(3,2)代入即可得出;
(2)设直线的方程
+
=1,把点P(3,2)代入可得
+
=1.利用基本不等式的性质即可得出.
| 2 |
| 3 |
(2)设直线的方程
| x |
| a |
| y |
| b |
| 3 |
| a |
| 2 |
| b |
解答:
解:(1)当直线经过原点时,可得直线方程为y=
x.
当直线不经过原点时,可设直线方程为x+y=a,把点(3,2)代入可得3+2=a,可得a=5.∴直线方程为x+y=5.
综上可得直线方程为:y=
x,x+y=5.
(2)设直线的方程
+
=1,把点P(3,2)代入可得
+
=1.
∴1≥2
,化为ab≥24,当且仅当
=
=
,即a=6,b=4时取等号.
∴△ABO的面积的最小值为
ab=12,此时直线l的方程为
+
=1.
| 2 |
| 3 |
当直线不经过原点时,可设直线方程为x+y=a,把点(3,2)代入可得3+2=a,可得a=5.∴直线方程为x+y=5.
综上可得直线方程为:y=
| 2 |
| 3 |
(2)设直线的方程
| x |
| a |
| y |
| b |
| 3 |
| a |
| 2 |
| b |
∴1≥2
|
| 3 |
| a |
| 2 |
| b |
| 1 |
| 2 |
∴△ABO的面积的最小值为
| 1 |
| 2 |
| x |
| 6 |
| y |
| 4 |
点评:本题考查了直线的截距式、基本不等式的性质、三角形的面积计算公式,考查了分类讨论的思想方法,考查了计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=min{2
, |x-2|},其中min{a,b}=
,若动直线y=m与函数y=f(x)的图象有三个不同的交点,它们的横坐标分别为x1、x2、x3,则x1+x2+x3的取值范围是( )
| x |
|
A、(2,6-2
| ||
B、(2,
| ||
C、(4,8-2
| ||
D、(0,4-2
|
如图,矩形ABCD中,AB=2AD=2,点p在以AB为直径的半圆上移动,若
=λ
,则λ+μ的最大值是( )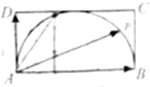
| AP |
| AD |

A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|