题目内容
9.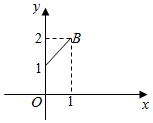 设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.
设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.
分析 根据条件求出函数f(x)的解析式,利用函数与方程的关系进行转化求解即可.
解答 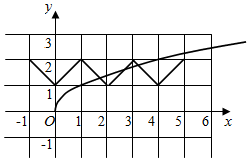 解:由图象知,直线方程设y=kx+b,则$\left\{\begin{array}{l}{0+b=1}\\{k+b=2}\end{array}\right.$,即$\left\{\begin{array}{l}{b=1}\\{k=1}\end{array}\right.$,
解:由图象知,直线方程设y=kx+b,则$\left\{\begin{array}{l}{0+b=1}\\{k+b=2}\end{array}\right.$,即$\left\{\begin{array}{l}{b=1}\\{k=1}\end{array}\right.$,
则AB的方程为y=x+1,0≤x≤1,
∵函数f(x)是偶函数,
∴当-1≤x≤0时,0≤-x≤1,
则f(x)=f(-x)=-x+1,-1≤x≤0
当x≥0时,由[f(x)]2=x得f(x)=$\sqrt{x}$,
∵函数y=f(x)是最小正周期为2的偶函数,
∴作出函数f(x)和g(x)=$\sqrt{x}$的图象如图
由图象知f(5)=f(3)=f(1)=2,
g(3)=$\sqrt{3}$<2,g(5)=$\sqrt{5}$>2,
则当3≤x≤4时,方程f(x)=$\sqrt{x}$取得最大根,
当3≤x≤4时,-1≤x-4≤0,
则f(x)=f(x-4)=-(x-4)+1=-x+5,
由f(x)=$\sqrt{x}$得-x+5=$\sqrt{x}$,
平方得x2-10x+25=x,
即x2-11x+25=0,
得x=$\frac{11+\sqrt{1{1}^{2}-4×25}}{2}$=$\frac{11+\sqrt{21}}{2}$(舍)或x=$\frac{11-\sqrt{1{1}^{2}-4×25}}{2}$=$\frac{11-\sqrt{21}}{2}$
故答案为:$\frac{11-\sqrt{21}}{2}$
点评 本题主要考查函数与方程的应用,根据条件求出函数的解析式,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
20.(x2-x+1)3展开式中x项的系数为( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
17.(x2-x-2)6的展开式中x2的系数等于( )
| A. | -48 | B. | 48 | C. | 234 | D. | 432 |
4.已知复数z满足zi=2i+x(x∈R),若z的虚部为2,则|z|=( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
18.已知集合A={0,1},B={-1,0,a+2},且A⊆B,则实数a=( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
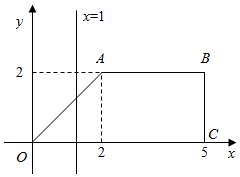 如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).
如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).