题目内容
14.若f(x)为二次函数,-1和3是方程f(x)-x-4=0的两根,f(0)=1(1)求f(x)的解析式;
(2)若在区间[-1,1]上,不等式f(x)>2x+m有解,求实数m的取值范围.
分析 (1)设二次函数f(x)=ax2+bx+c,(a≠0),由题意和韦达定理待定系数可得;
(2)问题转化为m<x2-3x+1在区间[-1,1]上有解,只需m小于函数g(x)=x2-3x+1在区间[-1,1]上的最大值,由二次函数区间的最值可得.
解答 解:(1)设二次函数f(x)=ax2+bx+c,(a≠0),
由f(0)=1可得c=1,
故方程f(x)-x-4=0可化为ax2+(b-1)x-3=0,
∵-1和3是方程f(x)-x-4=0的两根,
∴由韦达定理可得-1+3=-$\frac{b-1}{a}$,-1×3=$\frac{-3}{a}$,
解得a=1,b=-1,故f(x)的解析式为f(x)=x2-x+1;
(2)∵在区间[-1,1]上,不等式f(x)>2x+m有解,
∴m<x2-3x+1在区间[-1,1]上有解,
故只需m小于函数g(x)=x2-3x+1在区间[-1,1]上的最大值,
由二次函数可知当x=-1时,函数g(x)取最大值5,
∴实数m的取值范围为(-∞,5)
点评 本题考查函数解析式求解的方法,涉及韦达定理和二次函数区间的最值,属中档题.

练习册系列答案
相关题目
5.设x,y∈R,则(x-y)x4<0是x<y的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知集合M满足{1,2}⊆M?{1,2,3,4},则集合M的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
6.已知f(x)=lnx,则$f'(\frac{1}{e})$的值为( )
| A. | 1 | B. | -1 | C. | e | D. | $\frac{1}{e}$ |
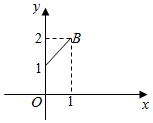 设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.
设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.