题目内容
17.(x2-x-2)6的展开式中x2的系数等于( )| A. | -48 | B. | 48 | C. | 234 | D. | 432 |
分析 先把多项式化简,再用二项式定理展开式中的通项求出特定项的系数,求出对应x2项的系数即可.
解答 解:(x2-x-2)6=(x+1)6(x-2)6,
(x+1)6的二项式定理的展开式的通项为Tr+1=C6rx6-r,
(x-2)6的二项式定理的展开式的通项为Tr+1=C6rx6-r•(-2)r
(x2-x-2)6展开式里x2的系数为:
C66(-2)6C64+C65(-2)5C65+C64(-2)4C66 =48.
故选:B.
点评 本题主要考查了二项式定理的应用以及利用二项式展开式的通项公式求展开式中某项的系数问题,是基础题目.

练习册系列答案
相关题目
8.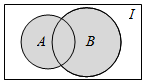 已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )
已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )
 已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )
已知如图,全集I=R,集合A={x|0<x<2},B={x|1<x<3},则图中阴影部分所表示的集合为( )| A. | {x|0<x<2} | B. | {x|0<x<3} | C. | {x|x<3} | D. | {x|x>0} |
5.设x,y∈R,则(x-y)x4<0是x<y的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知集合A={x|x2-5x+6≤0},B={x∈Z|2x>1},则A∩B=( )
| A. | [2,3] | B. | (0,+∞) | C. | (0,2)∪(3,+∞) | D. | (0,2]∪[3,+∞) |
6.已知f(x)=lnx,则$f'(\frac{1}{e})$的值为( )
| A. | 1 | B. | -1 | C. | e | D. | $\frac{1}{e}$ |
7.不等式4x2-4x+1≥0的解集为( )
| A. | {$\frac{1}{2}$} | B. | {x|x$≥\frac{1}{2}$} | C. | R | D. | ∅ |
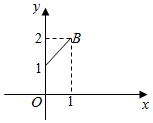 设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.
设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则方程[f(x)]2=x的最大实数根的值为$\frac{11-\sqrt{21}}{2}$.