题目内容
tan67°30′-tan22°30′= .
考点:三角函数的化简求值
专题:三角函数的求值
分析:首先,根据67°30′=90°-22°30′,然后,根据二倍角公式进行计算即可.
解答:
解:∵tan67°30′=tan(90°-22°30′)
=
∵tan22°30′=tan
×45°
=
=
-1,
∴tan67°30′-tan22°30′
=
-(
-1)
=
+1-(
-1)
=2
故答案为:2
=
| 1 |
| tan22°30′ |
∵tan22°30′=tan
| 1 |
| 2 |
=
| sin45° |
| 1+cos45° |
=
| 2 |
∴tan67°30′-tan22°30′
=
| 1 | ||
|
| 2 |
=
| 2 |
| 2 |
=2
故答案为:2
点评:本题重点考查了诱导公式、二倍角公式等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
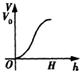
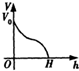
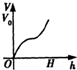
 一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )