题目内容
在△ABC中,6sinA+4cosB=1,且4sinB+6cosA=5
,则cosC=( )
| 3 |
A、
| ||||
B、±
| ||||
C、
| ||||
D、-
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:对已知两个方程平方相加,利用两角和与差的三角函数化简,结合同角三角函数的基本关系式即可求出结果.
解答:
解:6sinA+4cosB=1,且4sinB+6cosA=5
,
∴(6sinA+4cosB)2=1,…①,
(4sinB+6cosA)2=75,…②,
①+②可得:16+36+48(sinAcosB+cosAsinB)=76
∴sin(A+B)=
,
∴sinC=
.
∴cosC=±
,又∠C∈(0,π),
∴∠C的大小为
或
,
若∠C=
,得到A+B=
,则cosB>
,所以4cosB>2>1,sinA>0,
∴6sinA+4cosB>2与6sinA+4cosB=1矛盾,所以∠C≠
,
∴满足题意的∠C的值为
.
则cosC=
.
故选:C.
| 3 |
∴(6sinA+4cosB)2=1,…①,
(4sinB+6cosA)2=75,…②,
①+②可得:16+36+48(sinAcosB+cosAsinB)=76
∴sin(A+B)=
| 1 |
| 2 |
∴sinC=
| 1 |
| 2 |
∴cosC=±
| ||
| 2 |
∴∠C的大小为
| π |
| 3 |
| 2π |
| 3 |
若∠C=
| 2π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴6sinA+4cosB>2与6sinA+4cosB=1矛盾,所以∠C≠
| 2π |
| 3 |
∴满足题意的∠C的值为
| π |
| 3 |
则cosC=
| ||
| 2 |
故选:C.
点评:此题考查同角三角函数间基本关系的运用,注意角的范围的讨论,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
对于集合A={x|x=3m+2n,m,n∈Z},B={x|x=3m+8n,m,n∈Z},下列说法中正确的是( )
| A、A?B | B、A?B |
| C、A?Z,B?Z | D、A=B |
下列命题中真命题的个数有( )个
(1)“奇函数的图象关于原点对称”的逆命题
(2)“若ab=0,则a=0或b=0”的否命题是“若ab≠0,则a≠0且b≠0”
(3)ab≠0是a≠0的充分条件
(4)椭圆的离心率越大,椭圆越扁.
(1)“奇函数的图象关于原点对称”的逆命题
(2)“若ab=0,则a=0或b=0”的否命题是“若ab≠0,则a≠0且b≠0”
(3)ab≠0是a≠0的充分条件
(4)椭圆的离心率越大,椭圆越扁.
| A、1 | B、2 | C、3 | D、4 |
将函数y=5sin3x的图象向左平移π个单位,得到的图象的解析式是( )
A、y=5sin(3x+
| ||
B、y=5sin(3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |
直角三角形的斜边长为2,则其内切圆半径的最大值为( )
A、
| ||
B、
| ||
C、2
| ||
D、2(
|
已知a、b∈R,“a<b”是“2a<3b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
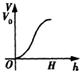
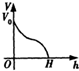
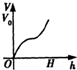
 一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )