题目内容
若沿△ABC三条边的中位线折起能拼成一个三棱锥,则△ABC( )
| A、一定是等边三角形 |
| B、一定是锐角三角形 |
| C、可以是直角三角形 |
| D、可以是钝角三角形 |
考点:棱锥的结构特征,三角形的形状判断
专题:空间位置关系与距离
分析:在三棱锥的展开图中:过底面任意一个顶点的三个角,应满足∠1+∠2>∠3,其中∠3为底面三角形的内角,进而逐一分析△ABC为不同形状时沿△ABC三条边的中位线能否拼成一个三棱锥,最后综合讨论结果,可得答案.
解答:
解:在三棱锥的展开图中:

过底面任意一个顶点的三个角,应满足∠1+∠2>∠3,
当△ABC为锐角三角形时,
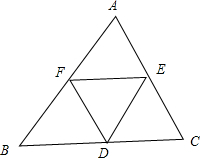
三个顶点处均满足此条件,故能拼成一个三棱锥,
当△ABC为锐角三角形时,
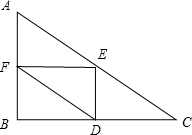
在斜边中点E处不满足条件,故不能拼成一个三棱锥,
同理当△ABC为钝角三角形时,
在钝角所对边中点处不满足条件,故不能拼成一个三棱锥,
综上可得:△ABC一定是锐角三角形,
故选:B

过底面任意一个顶点的三个角,应满足∠1+∠2>∠3,
当△ABC为锐角三角形时,

三个顶点处均满足此条件,故能拼成一个三棱锥,
当△ABC为锐角三角形时,

在斜边中点E处不满足条件,故不能拼成一个三棱锥,
同理当△ABC为钝角三角形时,
在钝角所对边中点处不满足条件,故不能拼成一个三棱锥,
综上可得:△ABC一定是锐角三角形,
故选:B
点评:本题考查的知识点是棱锥的结构特征,三角形形状的判断,其中正确理解:三棱锥的展开图中,过底面任意一个顶点的三个角,应满足∠1+∠2>∠3,其中∠3为底面三角形的内角,是解答的关键.

练习册系列答案
相关题目
将函数y=5sin3x的图象向左平移π个单位,得到的图象的解析式是( )
A、y=5sin(3x+
| ||
B、y=5sin(3x-
| ||
| C、y=5sin3x | ||
| D、y=-5sin3x |
直角三角形的斜边长为2,则其内切圆半径的最大值为( )
A、
| ||
B、
| ||
C、2
| ||
D、2(
|
已知cosα=-
,sinα=
,那么α的终边所在的象限为( )
| 3 |
| 5 |
| 4 |
| 5 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知a、b∈R,“a<b”是“2a<3b”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
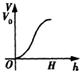
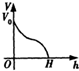
 一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
一高为H、满缸水量为V0的鱼缸的轴截面如图所示,其底部碰了一个小洞,满缸水从洞中流出,若鱼缸水深为h时水的体积为V,则函数的大致图象可能是( )
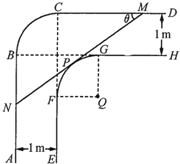 一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角处的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B,C两点,EF∥AB,GH∥CD且两组平行墙壁间的走廊宽度都是1m.