题目内容
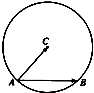
如图，在圆C中，若
•
=1，则弦AB的长度为 ．
| AB |
| AC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设圆的半径为r，AB=2d，由数量积的定义得到
•
=1=2dr
，解得d即可．
| AB |
| AC |
| d |
| r |
解答：
解：设圆的半径为r，AB=2d，所以
•
=1=2dr
，解得d=
，所以AB=
；
故答案为：
．
| AB |
| AC |
| d |
| r |
| ||
| 2 |
| 2 |
故答案为：
| 2 |
点评：本题考查了向量的数量积以及圆的半径、弦长、弦心距的关系，属于基础题．
练习册系列答案
相关题目
已知O是等边△ABC边AC（不含端点）上的一点，D为AB上的点，且|
|=2|
|=2，
+
=2
，则
•
=（ ）
| AB |
| OD |
| OA |
| OB |
| OD |
| AO |
| OD |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
已知函数f（x）=cosx，x∈（0，2π）有两个不同的零点x1，x2，且方程f（x）=m（m≠0）有两个不同的实根x3，x4，若把这四个数按从小到大排列构成等差数列，则实数m=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
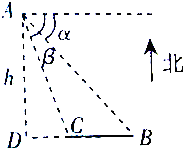如图，从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β，此时气球的高度为h，则两个场馆B、C间的距离为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图过拋物线y2=2px（p＞0）的焦点F的直线依次交拋物线及准线于点A，B，C，若|BC|=2|BF|，且|AF|=3，则拋物线的方程为（ ）A、y2=
| ||
| B、y2=3x | ||
C、y2=
| ||
| D、y2=9x |