题目内容
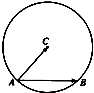
已知O是等边△ABC边AC（不含端点）上的一点，D为AB上的点，且|
|=2|
|=2，
+
=2
，则
•
=（ ）
| AB |
| OD |
| OA |
| OB |
| OD |
| AO |
| OD |
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：充分利用等边三角形的性质，结合已知容易得到OB⊥AC，OD是直角△AOB的斜边的中点，由此利用向量的数量积可求．
解答：
解：因为已知O是等边△ABC边AC（不含端点）上的一点，D为AB上的点，且|
|=2|
|=2，
+
=2
，
所以BO⊥AC，OD是△AOB的中线，所以∠AOD=60°，所以
•
=AO×OD×cos120°=-1×1×
=-
；
故选A．
| AB |
| OD |
| OA |
| OB |
| OD |
所以BO⊥AC，OD是△AOB的中线，所以∠AOD=60°，所以
| AO |
| OD |
| 1 |
| 2 |
| 1 |
| 2 |
故选A．
点评：本题考查了等边三角形的性质以及三角形中线的性质，关键是求出
，
的夹角，利用向量的数量积求之．
| AO |
| OD |
练习册系列答案
相关题目
若数列{an}满足：a1=1，an+1=2an（n∈N*），则a5=（ ）
| A、8 | B、16 | C、32 | D、9 |