Question

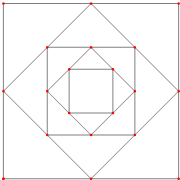如图，画一个边长为10cm的正方形，再将这个正方形各边的中点相连得到第二个正方形，依此类推，这样一共画了五个正方形，则它们的面积的和为（　　）

• A、193.75cm²
• B、387.5cm²
• C、187.5cm²
• D、200.75cm²

Answer 1

考点：等比数列的前n项和

专题：等差数列与等比数列

分析：结合图形发现：每一个小正方形的面积都是前边正方形的面积的

1

2

．他们构造一个等比数列，根据等比数列的前n项和公式即可得到结论．

解答： 解：观察图形发现：第二个正方形的边长为5

2

，面积为(5

2

)2=50，第一个正方形的面积S=100，
每一个最小正方形的面积都是前边正方形的面积的

1

2

，
则对应正方形的面积构成等比数列，公比q=

1

2

，首项为100，
则S5=

100[1-( 1 2 )5]

1- 1 2

=200×

31

32

=193.75，
故选：A

点评：本题主要考查等比数列的前n项和的计算，根据正方形的面积公式得到面积关系是解决本题的关键．