题目内容
如图，已知⊙O是△ABC的外接圆，AB＝BC，AD是BC边上的高，AE是⊙O的直径．
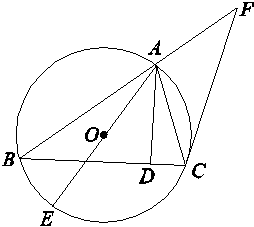
(1)求证：AC·BC＝AD·AE；
(2)过点C作⊙O的切线交BA的延长线于点F，若AF＝4，CF＝6，求AC的长．
(1)证明：连接BE，则△ABE为直角三角形，
因为∠ABE＝∠ADC＝90°，∠AEB＝∠ACB，
所以△ABE∽△ADC，
则
，
即AB·AC＝AD·AE.
又AB＝BC，
所以AC·BC＝AD·AE.
(2)因为FC是⊙O的切线，
所以FC2＝AF·BF.
又AF＝4，CF＝6，
则BF＝9，AB＝BF－AF＝5.
因为∠ACF＝∠CBF，又∠CFB＝∠AFC，
所以△AFC∽△CFB，
则
，即AC＝
＝
.
练习册系列答案
相关题目
；命题q：∀x∈(0，＋∞)，x2－2ax＋1≥0.若命题p∧q为真，则实数a的取值范围是________．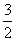
(an－1)，数列{bn}满足bn＝
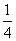bn－1－
(n≥2)，且b1＝3.
≤k恒成立，求k的取值范围．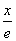
＋
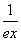(e≈2.718…)．
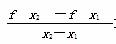＞0；
＝________．
＝0，
＝0，则该四边形一定是________．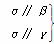
⇒β∥γ ②
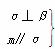⇒m⊥β ③
⇒α⊥β ④
⇒m∥α