已知f(x)＝|ax+1|(a∈R).不等式f(x)≤3的解集为{x|-2≤x≤1}． (1)求a的值, (2)若≤k恒成立.求k的取值范围．题目和参考答案——青夏教育精英家教网——

题目内容

已知f(x)＝|ax＋1|(a∈R)，不等式f(x)≤3的解集为{x|－2≤x≤1}．

(1)求a的值；

(2)若≤k恒成立，求k的取值范围．

解析：(1)由|ax＋1|≤3，得－4≤ax≤2.

又f(x)≤3的解集为{x|－2≤x≤1}，

所以当a≤0时，不合题意．

当a＞0时，－≤x≤，得a＝2.

(2)记h(x)＝f(x)－2f，

则h(x)＝

所以|h(x)|≤1，因此k≥1.

故k的取值范围是[1，＋∞)．

练习册系列答案

名师指导考出好成绩系列答案

期末第1卷系列答案

轻松夺冠优胜卷系列答案

清华绿卡核心密卷系列答案

全能卷王单元测试卷系列答案

全能练考卷系列答案

随堂优化训练系列答案

王朝霞培优100分系列答案

无敌战卷系列答案

小学生绩优名卷系列答案

相关题目

已知R是实数集，集合A＝{y|y＝x²－2x＋2，x∈R，－1≤x≤2}，集合B＝，任取x∈A，则x∈A∩B的概率等于________．

如图，在三棱锥O－ABC中，三条棱OA，OB，OC两两垂直，

且OA＞OB＞OC，分别经过三条棱OA，OB，OC作一个截面平分三棱锥的体积，截面面积依次为S₁，S₂，S₃，则S₁，S₂，S₃的大小关系为________．

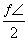已知函数y＝Asin(ωx＋φ)＋k(A＞0)的最大值为4，最小值为0，最小正周期为，直线x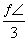＝是其图象的一条对称轴，则下面各式中符合条件的解析式为(　　)

A．y＝4sin　　 B．y＝2sin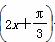＋2

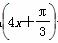C．y＝2sin＋2 D．y＝2sin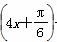＋2

已知a²sin θ＋acos θ－2＝0，b²sin θ＋bcos θ－2＝0(a，b，θ∈R，且a≠b)，直线l过点A(a，a²)，B(b，b²)，则直线l被圆(x－cos θ)²＋(y－sin θ)²＝4所截得的弦长为________．

已知函数f(x)＝|x－2|＋2|x－a|(a∈R)．

(1)当a＝1时，解不等式f(x)＞3；

(2)不等式f(x)≥1在区间(－∞，＋∞)上恒成立，求实数a的取值范围．

如图，已知⊙O是△ABC的外接圆，AB＝BC，AD是BC边上的高，AE是⊙O的直径．

(1)求证：AC·BC＝AD·AE；

(2)过点C作⊙O的切线交BA的延长线于点F，若AF＝4，CF＝6，求AC的长．

若复数z＝1＋i(i为虚数单位)，是z的共轭复数，则z²＋²的虚部为________．

在△ABC中，已知a、b、c分别为内角A、B、C所对的边，S为△ABC的面积．若向量p＝(4，a²＋b²－c²)，q＝(1，S)满足p∥q，则C＝________．