题目内容
已知函数f(x)=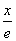 +
+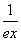 (e≈2.718…).
(e≈2.718…).
(1)若x1,x2∈[1,+∞),x1≠x2,求证: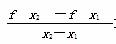 >0;
>0;
(2)若满足f(|a|+3)>f(|a-4|+1),试求实数a的取值范围.
(1)证明:
∵ x1,x2∈[1,+∞),x1≠x2,
∴ x1x2>1>0,∴ >0.
>0.
∴ >0.
>0.
(2)由(1)可知,f(x)在[1,+∞)上为单调增函数.
∵ |a|+3>1,|a-4|+1≥1且f(|a|+3)>f(|a-4|+1),
∴ |a|+3>|a-4|+1.
当a≤0时,有-a+3>4-a+1,∴ 3>5,
∴ a无解;
当0<a<4时,有a+3>4-a+1,∴ a>1,
∴ 1<a<4;
当a≥4时,a+3>a-4+1,∴ 3>-3,∴ a≥4.
综上所述:a的取值范围是(1,+∞).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
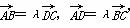 ”是“四边形ABCD为平行四边形”的( )
”是“四边形ABCD为平行四边形”的( ) (n∈N*),则a20=( )
(n∈N*),则a20=( )


 +i,ω=sinθ-icosθ(θ∈R).求z的值和|z-ω|的取值范围.
+i,ω=sinθ-icosθ(θ∈R).求z的值和|z-ω|的取值范围. ,求
,求 +
+ 的值.
的值.