题目内容
数列{an}的前n项和为Sn,且Sn=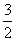 (an-1),数列{bn}满足bn=
(an-1),数列{bn}满足bn=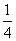 bn-1-
bn-1- (n≥2),且b1=3.
(n≥2),且b1=3.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}满足cn=an·log2(bn+1),其前n项和为Tn,求Tn.
解析:(1)对于数列{an}有Sn=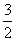 (an-1),①
(an-1),①
Sn-1=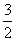 (an-1-1)(n≥2),②
(an-1-1)(n≥2),②
由①-②,得an=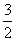 (an-an-1),即an=3an-1,
(an-an-1),即an=3an-1,
n=1时,S1=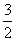 (a1-1)=a1,解得a1=3,
(a1-1)=a1,解得a1=3,
则an=a1·qn-1=3·3n-1=3n.
对于数列{bn},有bn=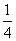 bn-1-
bn-1- (n≥2),
(n≥2),
可得bn+1=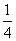 bn-1+
bn-1+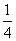 ,即
,即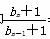 =
=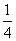 .
.
bn+1=(b1+1)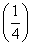 n-1=4
n-1=4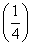 n-1=42-n,
n-1=42-n,
即bn=42-n-1.
(2)由(1)可知
cn=an·log2(bn+1)=3n·log2 42-n
=3n·log2 24-2n=3n(4-2n).
Tn=2·31+0·32+(-2)·33+…+(4-2n)·3n,③
3Tn=2·32+0·33+…+(6-2n)·3n+(4-2n)·3n+1,④
由③-④,得
-2Tn=2·3+(-2)·32+(-2)·33+…+(-2)·3n-(4-2n)·3n+1
=6+(-2)(32+33+…+3n)-(4-2n)·3n+1,
则Tn=-3+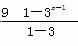 +(2-n)·3n+1
+(2-n)·3n+1
=-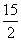 +
+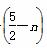 ·3n+1.
·3n+1.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目

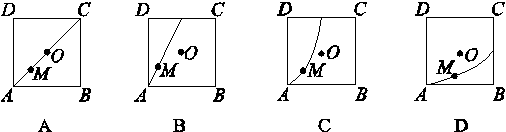
 (n∈N*),则a20=( )
(n∈N*),则a20=( )

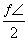 ,直线x=
,直线x=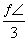 是其图象的一条对称轴,则下面各式中符合条件的解析式为( )
是其图象的一条对称轴,则下面各式中符合条件的解析式为( ) B.y=2sin
B.y=2sin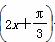 +2
+2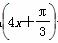 +2 D.y=2sin
+2 D.y=2sin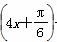 +2
+2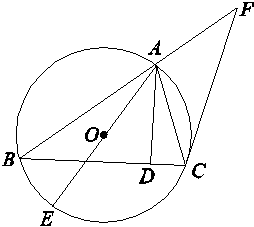
 ,BC=2,点E为BC的中点,点F在边CD上.若
,BC=2,点E为BC的中点,点F在边CD上.若 =
= =________.
=________.