题目内容
某几何体的三视图如图所示(网格中的小正方形边长为1),则该几何体的表面积为( )


A、6+2
| ||||
B、4+4
| ||||
C、2+4
| ||||
D、4+2
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图,得出该几何体的结构特征是什么,由此求出表面积.
解答:
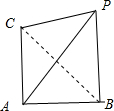 解:由三视图知,该几何体是一个三棱锥,
解:由三视图知,该几何体是一个三棱锥,
该三棱锥中,侧棱PA⊥底面ABC,底面△ABC中,AB=AC=2,∠BAC=90°,如图所示;
∴S△PAB=
•AB•PB=
×2×2=2
S△ABC=
•AB•AC=
×2×2=2
S△PBC=
•PB•BC=
×2×
=2
S△PAC=
•PA•AC=
×
×2=2
∴的表面积是S=S△PAB+S△ABC+S△PBC+S△PAC=2+2+2
+2
=4+4
,
故选:B.
 解:由三视图知,该几何体是一个三棱锥,
解:由三视图知,该几何体是一个三棱锥,该三棱锥中,侧棱PA⊥底面ABC,底面△ABC中,AB=AC=2,∠BAC=90°,如图所示;
∴S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 22+22 |
| 2 |
S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 22+22 |
| 2 |
∴的表面积是S=S△PAB+S△ABC+S△PBC+S△PAC=2+2+2
| 2 |
| 2 |
| 2 |
故选:B.
点评:本题考查了几何体的三视图的应用问题,解题时应根据三视图得出几何体的结构特征,是基础题目.

练习册系列答案
相关题目
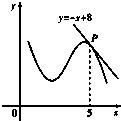 如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )| A、2 | ||
| B、1 | ||
C、
| ||
| D、0 |
已知直线l的一个方向向量为
=(1,-1,-2),平面α的一个法向量为
=(2,-2,-4),则( )
| a |
| b |
| A、l∥α |
| B、l?α |
| C、l⊥α |
| D、直线l与平面α相交但不垂直 |
在△ABC中,过中线AD的中点E任作一条直线分别交AB,AC于M,N两点,若
=x
,
=y
,则4x+y的最小值为( )
| AM |
| AB |
| AN |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
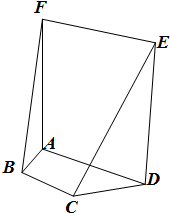 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2