题目内容
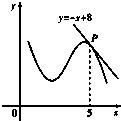如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=（ ）| A、2 | ||
| B、1 | ||
C、
| ||
| D、0 |
考点：利用导数研究曲线上某点切线方程
专题：圆锥曲线的定义、性质与方程
分析：根据导数的几何意义知，函数y=f（x）的图象在点P处的切线的斜率就是函数y=f（x）在该点的导数值，因此可求得f′（5）．
解答：
解：根据图象知，函数y=f（x）的图象与在点P处的切线交于点P，
f（5）=-5+8=3，
f′（5）为函数y=f（x）的图象在点P处的切线的斜率，
∴f′（5）=-1；
∴f（5）+f′（5）=2．
故选：A．
f（5）=-5+8=3，
f′（5）为函数y=f（x）的图象在点P处的切线的斜率，
∴f′（5）=-1；
∴f（5）+f′（5）=2．
故选：A．
点评：本题是基础题．考查导数的几何意义以及学生识图能力的考查，命题形式新颖，值得收藏．
练习册系列答案
初中学业考试导与练系列答案
相关题目
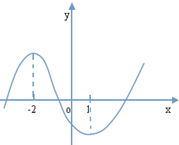
如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是Ac，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到A1DE的位置，使A1C⊥CD，如图2．已知函数f（x）=ax3+bx2+cx+d的图象如图所示，其导函数是f′（x），则
=（ ）
| f′(3) |
| f′(-1) |
| A、-2 | B、2 | C、5 | D、-5 |
某几何体的三视图如图所示（网格中的小正方形边长为1），则该几何体的表面积为（ ）
A、6+2
| ||||
B、4+4
| ||||
C、2+4
| ||||
D、4+2
|