Question

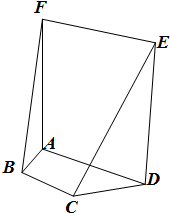如图，在五面体ABCDEF中，四边形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=2

2

，∠BAD=∠CDA=45°．
（Ⅰ）求异面直线CE与AF所成角的余弦值；
（Ⅱ）求证：平面CDE⊥平面ABF；
（Ⅲ）求五面体ABCDEF的体积．

Answer 1

考点：棱柱、棱锥、棱台的体积,异面直线及其所成的角,平面与平面垂直的判定

专题：空间位置关系与距离

分析：（Ⅰ）以A为坐标原点，AD所在直线为y轴，AF所在直线为z 轴，建立空间直角坐标系如图所示，利用向量法能求出异面直线CE与AF所成角的余弦值．
（Ⅱ）过B点作BG∥CD，交AC于点G，由已知得CD⊥AB，FA⊥CD，从而CD⊥平面ABF，由此能证明平面CDE⊥平面ABF．
（Ⅲ）五面体ABCDEF的体积V=V_F-ABCD+V_C-DEF，由此能求出结果．

解答： （本小题满分12分）
（Ⅰ）解：以A为坐标原点，AD所在直线为y轴，AF所在直线为z 轴，
建立空间直角坐标系如图所示，
则A（0，0，0），C（

2

2

，

3 2

2

，0），
E（0，2

2

，2

2

），F（0，0，2

2

），

CE

=（-

2

2

，

2

2

，2

2

），

AF

=（0，0，2

2

），
设异面直线CE与AF所成角为θ，
cosθ=|cos＜

CE

，

AF

＞|=|

8

9 •2 2

|=

2 2

3

．
（Ⅱ）证明：过B点作BG∥CD，交AC于点G，
由已知得BG⊥AB，∴CD⊥AB，
又∵FA⊥平面ABCD，CD?平面ABCD，
∴FA⊥CD，又AB∩FA=A，∴CD⊥平面ABF，
又CD?平面CDE，∴平面CDE⊥平面ABF．
（Ⅲ）解：由已知得AD=FA=2

2

，FA⊥平面ABCD，
BC=

2

，C到平面DEF的距离d=

2

2

，
S_梯形ABCD=

1

2

(2

2

+

2

)×

2

2

=

3

2

，
S_△DEF=

1

2

×2

2

×2

2

=4，
∴五面体ABCDEF的体积：
V=V_F-ABCD+V_C-DEF
=

1

3

S梯形ABCD×AF+

1

3

S△DEF×d
=

1

3

×

3

2

×2

2

+

1

3

×4×

2

2

=

5 2

3

．

点评：本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识，考查空间想象能力，运算能力和推理论证能力．