Question

如图，已知椭圆E：

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

1

2

，且经过点P（1，

3

2

）．
（1）求椭圆E的方程；
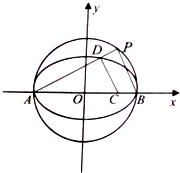
（2）O为坐标原点，A，B，C是椭圆E上不同的三点，并且O为△ABC的重心，试探究△ABC的面积是否为定值，若是，求出这个定值，若不是，说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：探究型,圆锥曲线的定义、性质与方程

分析：（1）运用椭圆的离心率公式，和椭圆的方程，结合a²-b²=c²，求出a，b，c．
（2）设直线AB的方程为y=kx+m，联立椭圆方程，消去y，得到x的方程，运用韦达定理，求出x₁+x₂，y₁+y₂，运用重心公式，

OA

+

OB

+

OC

=

0

，再运用弦长公式|AB|=

1+k2

|x1-x2|，再运用面积公式即可得到结论．

解答： 解：（1）依题意，e=

c

a

=

1

2

，且

1

a2

+

9

4b2

=1，a²-b²=c²，
∴a=2，b=

3

，c=1，
∴椭圆E的方程为

x2

4

+

y2

3

=1；
（2）设直线AB的方程为y=kx+m，
由

x2 4 + y2 3 =1 y=kx+m

得，（3+4k²）x²+8kmx+4m²-12=0，
∴

x1+x2= -8km 3+4k2 x1x2= 4m2-12 3+4k2

，∴y₁+y₂=k（x₁+x₂）+2m=

6m

3+4k2

，
∵O为重心，∴

OC

=-(

OA

+

OB

)=(

8km

3+4k2

，

-6m

3+4k2

)，
∵C在椭圆上，∴

( 8km 3+4k2 )2

4

+

( -6m 3+4k2 )2

3

=1，
可得，4m²=4k²+3，
而|AB|=

1+k2

( -8km 3+4k2 )2-4•( 4m2-12 3+4k2 )

=

4 1+k2

3+4k2

12k2+9-3m2

d=

|kxC+m-yC|

1+k2

=

|3m|

1+k2

（或利用d是O到AB的距离的3倍得到）
∴S_△ABC=

1

2

|AB|•d=

6|m|

3+4k2

12k2+9-3m2

=

6|m|

4m2

12m2-3m2

=

9

2

若直线AB的斜率不存在时，|AB|=3，d=3，S_△ABC=

9

2

，
∴△ABC的面积为定值

9

2

．

点评：本题主要考查直线与椭圆的位置关系，以及弦长公式的运用，同时考查椭圆的方程和几何性质，考查运算能力．