题目内容
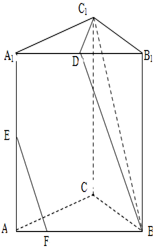 在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且AB=4AF.
在正三棱柱ABC-A1B1C1中,AB=AA1,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且AB=4AF.(1)求证:EF∥平面BDC1;
(2)求证:BC1⊥平面B1CE.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取AB的中点M,因为AB=4AF,所以F为AM的中点,进而根据三角形中位线定理,及平行四边形的性质得到EF∥BD,进而由线面平行的判定定理,得到EF∥平面BDC1;
(2)连接CE,B1E,B1C,根据等边三角形三线合一及直棱柱的几何特征,结合面面垂直的判定定理,可得C1D⊥B1E,进而四边形ABB1A1为正方形,BD⊥B1E,进而可得B1E⊥面C1DB,即BC1⊥B1E,又因为在正方形BB1C1C中,BC1⊥B1C,结合线面垂直的判定定理可得BC1⊥面B1CE.
(2)连接CE,B1E,B1C,根据等边三角形三线合一及直棱柱的几何特征,结合面面垂直的判定定理,可得C1D⊥B1E,进而四边形ABB1A1为正方形,BD⊥B1E,进而可得B1E⊥面C1DB,即BC1⊥B1E,又因为在正方形BB1C1C中,BC1⊥B1C,结合线面垂直的判定定理可得BC1⊥面B1CE.
解答:
证明:(1)取AB的中点M,
因为AB=4AF,
所以F为AM的中点,
又因为E为AA1的中点,
所以EF∥A1M,…(2分)
在正三棱柱ABC-A1B1C1中,D,M分别为A1B1,AB的中点,
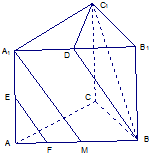
所以A1D∥BM,且A1D=BM,
则四边形A1DBM为平行四边形,
所以A1M∥BD,
所以EF∥BD,…(5分)
又因为BD?平面BDC1,EF?平面BDC1,
所以,EF∥平面BDC1 …(7分)
(2)连接CE,B1E,B1C,
因为在正三角A1B1C1中,D为A1B1的中点,
所以,C1D⊥A1B1,
所以,在正三棱柱ABC-A1B1C1中,C1D⊥面ABB1A1,
所以,C1D⊥B1E,
因为AA1=AB,
所以,四边形ABB1A1为正方形,由D,E分别为A1B1,AA1的中点,
所以,可证得BD⊥B1E,

所以,B1E⊥面C1DB,即BC1⊥B1E,…(11分)
又因为在正方形BB1C1C中,BC1⊥B1C,所以BC1⊥面B1CE,…(14分)
因为AB=4AF,
所以F为AM的中点,
又因为E为AA1的中点,
所以EF∥A1M,…(2分)
在正三棱柱ABC-A1B1C1中,D,M分别为A1B1,AB的中点,

所以A1D∥BM,且A1D=BM,
则四边形A1DBM为平行四边形,
所以A1M∥BD,
所以EF∥BD,…(5分)
又因为BD?平面BDC1,EF?平面BDC1,
所以,EF∥平面BDC1 …(7分)
(2)连接CE,B1E,B1C,
因为在正三角A1B1C1中,D为A1B1的中点,
所以,C1D⊥A1B1,
所以,在正三棱柱ABC-A1B1C1中,C1D⊥面ABB1A1,
所以,C1D⊥B1E,
因为AA1=AB,
所以,四边形ABB1A1为正方形,由D,E分别为A1B1,AA1的中点,
所以,可证得BD⊥B1E,

所以,B1E⊥面C1DB,即BC1⊥B1E,…(11分)
又因为在正方形BB1C1C中,BC1⊥B1C,所以BC1⊥面B1CE,…(14分)
点评:本题考查的知识点是直线与平面平行的判定定理,直线与平面垂直的判定定理和性质定理,难度不大,属于中档题.

练习册系列答案
相关题目
已知p:0≤x≤1,q:
<1,则p是q的( )
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
 如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h.
如图,某工厂生产的一种无盖冰淇淋纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π.设圆锥纸筒底面半径为r,高为h. 甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
甲、乙两名运动员为了争取得到2016年巴西奥运会的最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.