题目内容
设数列{an}前n项和为Sn,若已知点(n,
)均在函数y=x+1图象上,
(1)求数列{an}的通项公式;
(2)设bn=
,设Tn是{bn}前n项和,求使m>Tn对所有n∈N*都成立的m的取值范围.
| Sn |
| n |
(1)求数列{an}的通项公式;
(2)设bn=
| 4 |
| anan+1 |
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(1)由已知得到数列递推式,即数列的前n项和,则数列的通项公式可求;
(2)把(1)中求得的通项代入bn=
,整理后利用裂项相消法求和,求出Tn的范围,则答案可求.
(2)把(1)中求得的通项代入bn=
| 4 |
| anan+1 |
解答:
解:(1)由条件知
=2n-1,
即Sn=2n2-n,
当n≥2时,an=Sn-Sn-1=4n-3.
又n=1时,a1=s1=1符合上式,
∴an=4n-3(n∈N*);
(2)bn=
=
=
-
.
∴Tn=1-
+
-
+
-
+…+
-
=1-
=
=1-
<1.
∴m≥1.
即使m>Tn对所有n∈N*都成立的m的取值范围是[1,+∞).
| Sn |
| n |
即Sn=2n2-n,
当n≥2时,an=Sn-Sn-1=4n-3.
又n=1时,a1=s1=1符合上式,
∴an=4n-3(n∈N*);
(2)bn=
| 4 |
| anan+1 |
| 4 |
| (4n-3)(4n+1) |
| 1 |
| 4n-3 |
| 1 |
| 4n+1 |
∴Tn=1-
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 13 |
| 1 |
| 4n-3 |
| 1 |
| 4n+1 |
| 1 |
| 4n+1 |
| 4n |
| 4n+1 |
| 1 |
| 4n+1 |
∴m≥1.
即使m>Tn对所有n∈N*都成立的m的取值范围是[1,+∞).
点评:本题考查了由数列的前n项和求数列的通项,考查了裂项相消法求数列的和,是中档题.

练习册系列答案
相关题目
设全集为实数集R,集合A={x|x<2},B={x|x≥3},则( )
| A、A∪(∁RB)=R |
| B、(∁RA)∪(∁RB)=R |
| C、A∩(∁RB)=ϕ |
| D、∁R(A∪B)=ϕ |
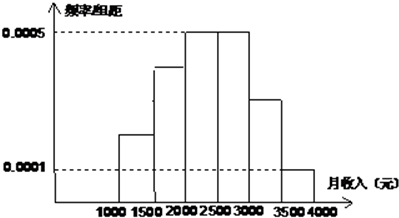
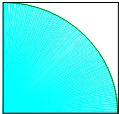 如图:在边长为2正方形内有一扇形(见阴影部分),点P随意等可能落在正方形内,
如图:在边长为2正方形内有一扇形(见阴影部分),点P随意等可能落在正方形内,