题目内容
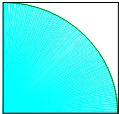如图：在边长为2正方形内有一扇形（见阴影部分），点P随意等可能落在正方形内，则这点落在扇形外且在正方形内的概率为
考点：几何概型
专题：概率与统计
分析：确定正方形、扇形的面积，结合几何概型的计算公式即可求得点落在扇形外且在正方形内的概率．
解答：
解：令正方形的边长为a，则S正方形=a2，
则扇形所在圆的半径也为a，则S扇形=
πa2
则黄豆落在阴影区域内的概率P=1-
=
．
故答案为：
则扇形所在圆的半径也为a，则S扇形=
| 1 |
| 4 |
则黄豆落在阴影区域内的概率P=1-
| S扇形 |
| S正方形 |
| 4-π |
| 4 |
故答案为：
| 4-π |
| 4 |
点评：本题主要考查扇形面积公式、几何概型等基础知识，考查运算求解能力，考查数形结合思想．解题的关键是要求出阴影部分的面积及正方形的面积，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知Rt△ABC，∠C=90°，CA=3，CB=4，点D、E在AB上，满足
=
，
=-
，则
•
=（ ）
| AD |
| 1 |
| 3 |
| AB |
| BE |
| 1 |
| 4 |
| AB |
| CE |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
若f（x）为定义在R上的偶函数，且f（x+2）=f（x），当x∈[0，1]时，f（x）=x2+1，则当 x∈[3，5]时，f（x）=（ ）
| A、（x+3）2+1 |
| B、（x-3）2+1 |
| C、（x-4）2+1 |
| D、（x-5）2+1 |
袋中装有6个白球，4个红球，从中任取1球，抽到白球的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、非以上答案 |
过点（3，2），且平行于直线x-2y+3=0（ ）
| A、x-2y+7=0 |
| B、2x+y-8=0 |
| C、x-2y+1=0 |
| D、2x+y-5=0 |
已知a，b，c分别是△ABC的三内角A，B，C所对的边，若a=1，b=
，B=
，则sinC的值为（ ）
| 3 |
| π |
| 3 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|