题目内容
设S={1，2，3，4}，n项的数列a1，a2，…an有下列性质：对于S的任何一个非空子集B，在该数列中有相邻的card（B）项恰好组成集合B，求n的最小值．
考点：元素与集合关系的判断
专题：集合,推理和证明
分析：根据已知中对于S的任何一个非空子集B，在该数列中有相邻的card（B）项恰好组成集合B，列举出满足条件的数列B，进而可得答案．
解答：
解：∵对于S的任何一个非空子集B，在该数列中有相邻的card（B）项恰好组成集合B，
故满足条件的数列至少为：1，2，3，4，1，3，2，1，4，
即n的最小值为：9
故满足条件的数列至少为：1，2，3，4，1，3，2，1，4，
即n的最小值为：9
点评：本题考查的知识点是集合和逻辑推理，其中正确理解性质：对于S的任何一个非空子集B，在该数列中有相邻的card（B）项恰好组成集合B，是解答的关键．
练习册系列答案
小夫子全能检测系列答案
相关题目
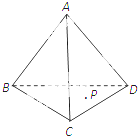如图，在四面体A-BCD中，△BCD是正三角形，侧棱AB、AC、AD两两垂直且相等，设P为四面体A-BCD表面（含棱）上的一点，由点P到四个顶点的距离组成的集合记为M，如果集合M中有且只有2个元素，那么符合条件的点P有（ ）| A、4个 | B、6个 | C、8个 | D、14个 |
直线x+
y-m=0与圆x2+y2=1在第一象限内有两个不同的交点，则m的取值范围是（ ）
| 3 |
| A、（1，2） | ||
B、（
| ||
C、（1，
| ||
D、（
|
已知0＜b＜1，0＜α＜
，x=(sinα)logbsinα，y=(cosα)logbcosα，z=(sinα)logbcosα则三数的大小关系是（ ）
| π |
| 4 |
| A、x＜y＜z |
| B、z＜x＜y |
| C、x＜z＜y |
| D、y＜z＜x |