题目内容
已知向量
=(sinx,
sinx),
=(sinx,cosx),设函数f(x)=
•
.
(Ⅰ)求函数f(x)的解析式,并求f(x)在区间[-
,
]上的最小值;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若f(A)+f(-A)=
,b+c=7,△ABC的面积为2
,求a.
| m |
| 3 |
| n |
| m |
| n |
(Ⅰ)求函数f(x)的解析式,并求f(x)在区间[-
| π |
| 4 |
| π |
| 6 |
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若f(A)+f(-A)=
| 3 |
| 2 |
| 3 |
考点:平面向量的综合题
专题:三角函数的求值,三角函数的图像与性质,解三角形,平面向量及应用
分析:(I)由向量
=(sinx,
sinx),
=(sinx,cosx),函数f(x)=
•
.结合向量的数量积运算定义及倍角公式,和差角公式,可得函数f(x)的解析式,进而由正弦型函数的图象和性质得到f(x)在区间[-
,
]上的最小值;
(Ⅱ)由A为锐角,f(A)+f(-A)=
,可求出A,结合△ABC的面积为2
,可求出bc,进而由余弦定理得到a值.
| m |
| 3 |
| n |
| m |
| n |
| π |
| 4 |
| π |
| 6 |
(Ⅱ)由A为锐角,f(A)+f(-A)=
| 3 |
| 2 |
| 3 |
解答:
解:(I)∵向量
=(sinx,
sinx),
=(sinx,cosx),
∴f(x)=
•
=sin2x+
sinxcos=
-
cos2x+
sin2x=sin(2x-
)+
,
∵x∈[-
,
],
∴2x-
∈[-
,
],
当2x-
=-
,即x=-
时,函数f(x)取最小值-
,
(II)∵f(A)+f(-A)=
,
∴sin(2A-
)+sin(-2A-
)+1=
,
化简得:cos2A=-
,
∵A为锐角,
∴2A=
,即A=
,
∵△ABC的面积为2
=
bcSinA=
bc,
∴bc=8,
∵b+c=7,
∴a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)=25,
∴a=5
| m |
| 3 |
| n |
∴f(x)=
| m |
| n |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∵x∈[-
| π |
| 4 |
| π |
| 6 |
∴2x-
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(II)∵f(A)+f(-A)=
| 3 |
| 2 |
∴sin(2A-
| π |
| 6 |
| π |
| 6 |
| 3 |
| 2 |
化简得:cos2A=-
| 1 |
| 2 |
∵A为锐角,
∴2A=
| 2π |
| 3 |
| π |
| 3 |
∵△ABC的面积为2
| 3 |
| 1 |
| 2 |
| ||
| 4 |
∴bc=8,
∵b+c=7,
∴a2=b2+c2-2bccosA=(b+c)2-2bc(1+cosA)=25,
∴a=5
点评:本题考查的知识点是平面向量的数量积,倍角公式,和差角公式,正弦函数的图象和性质,余弦定理,是三角函数,解三角形,向量的综合应用,难度较大.

练习册系列答案
相关题目
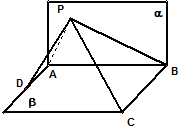 如图,已知平面α⊥平面β,α∩β=AB,C∈β,D∈β,DA⊥AB,CB⊥AB,BC=8,AB=6,AD=4,平面α有一动点P使得∠APD=∠BPC,则△PAB的面积最大值是( )
如图,已知平面α⊥平面β,α∩β=AB,C∈β,D∈β,DA⊥AB,CB⊥AB,BC=8,AB=6,AD=4,平面α有一动点P使得∠APD=∠BPC,则△PAB的面积最大值是( )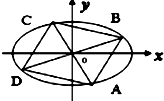 已知椭圆C1:
已知椭圆C1: 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.