题目内容
已知0＜b＜1，0＜α＜
，x=(sinα)logbsinα，y=(cosα)logbcosα，z=(sinα)logbcosα则三数的大小关系是（ ）
| π |
| 4 |
| A、x＜y＜z |
| B、z＜x＜y |
| C、x＜z＜y |
| D、y＜z＜x |
考点：不等式比较大小
专题：函数的性质及应用
分析：先利用对数f（x）=logbx的单调性比较x，z的大小，再利用指数函数比较z，y的大小．
解答：
解：由于0＜b＜1，∴函数f（x）=logbx是减函数，
又因为0＜α＜
，∴0＜sinα＜cosα＜1，
∴logbsinα＞logbcosα，
∴x=sinαlogbsinα＜sinαlogbcosα=z
又z=(sinα)logbcosα＜(cosα)logbcosα=y，
故选C．
又因为0＜α＜
| π |
| 4 |
∴logbsinα＞logbcosα，
∴x=sinαlogbsinα＜sinαlogbcosα=z
又z=(sinα)logbcosα＜(cosα)logbcosα=y，
故选C．
点评：本题主要指数函数的单调性和对数函数的单调性，利用他们的单调性判断函数值的大小，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
已知函数f（x）=
，若f（x）=ax有且只有一个实数解，则a的取值范围是（ ）
|
| A、[1，2] |
| B、（-∞，0] |
| C、（-∞，0]∪[1，2] |
| D、（-∞，2] |
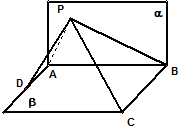如图，已知平面α⊥平面β，α∩β=AB，C∈β，D∈β，DA⊥AB，CB⊥AB，BC=8，AB=6，AD=4，平面α有一动点P使得∠APD=∠BPC，则△PAB的面积最大值是（ ）| A、24 | B、32 | C、12 | D、48 |
设f（x）是定义在R上的偶函数，对x∈R，都有f（x-2）=f（x+2），且当x∈[-2，0]时，f（x）=（
）x-1，若在区间（-2，6]内关于x的方程f（x）-loga（x+2）=0（a＞1）恰有3个不同的实根，则a的取值范围是（ ）
| 1 |
| 2 |
| A、（1，2） | |||
| B、（2，+∞） | |||
C、（1，
| |||
D、（
|
已知函数f（x）=
，若关于x的方程[f（x）]2+bf（x）+2=0有四个不同的正根，则b的取值范围是（ ）
| 1 |
| |x-1| |
A、（-∞，-2
| ||||
B、（-3，-2
| ||||
C、（-3，2
| ||||
D、（-2
|
sin2013°的值属于区间（ ）
A、（-
| ||
B、（-1，-
| ||
C、（
| ||
D、（0，
|