题目内容
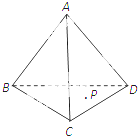如图，在四面体A-BCD中，△BCD是正三角形，侧棱AB、AC、AD两两垂直且相等，设P为四面体A-BCD表面（含棱）上的一点，由点P到四个顶点的距离组成的集合记为M，如果集合M中有且只有2个元素，那么符合条件的点P有（ ）| A、4个 | B、6个 | C、8个 | D、14个 |
考点：计数原理的应用,进行简单的合情推理
专题：计算题,推理和证明
分析：根据分类计数加法原理可得，由题意符合条件的点只有两类，一在棱的中点，二在面的外心，问题得以解决．
解答：
解：符合条件的点P有两类：（1）6条棱的中点；（2）4个面的外心．共10个点．
由于AB，AD的中点不行，AC的中点可以，BC，BD，CD的中点均可以，
还有△BCD的中心，△ABC，△ABD，△ACD的外心均可以．
故集合M中有且只有2个元素，那么符合条件的点P有4+4=8．
故选：C．
由于AB，AD的中点不行，AC的中点可以，BC，BD，CD的中点均可以，
还有△BCD的中心，△ABC，△ABD，△ACD的外心均可以．
故集合M中有且只有2个元素，那么符合条件的点P有4+4=8．
故选：C．
点评：本题主要考查了分类计数原理，简单的推理，关键是理解几何图形，属于基础题．
练习册系列答案
相关题目
用系统抽样法从已编好号码的500辆车中随机抽出5辆进行试验，则可能选取的车的编号是（ ）
| A、50、100、150、200、250 |
| B、13、113、213、313、413 |
| C、110、120、130、140、150 |
| D、12、40、80、160、320 |
已知函数f（x）=
，若f（x）=ax有且只有一个实数解，则a的取值范围是（ ）
|
| A、[1，2] |
| B、（-∞，0] |
| C、（-∞，0]∪[1，2] |
| D、（-∞，2] |
已知函数y=
在（-∞，-1）上为减函数，则a的范围为（ ）
| 1 |
| x-a |
| A、（-∞，-1） |
| B、（-1，+∞） |
| C、[-1，+∞） |
| D、（-∞，-1] |
在区间[0，10]上任取一个实数a，使得不等式2x2-ax+8≥0在（0，+∞）上恒成立的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
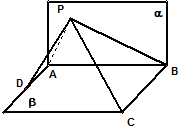如图，已知平面α⊥平面β，α∩β=AB，C∈β，D∈β，DA⊥AB，CB⊥AB，BC=8，AB=6，AD=4，平面α有一动点P使得∠APD=∠BPC，则△PAB的面积最大值是（ ）